定义
定义所谓 \(k\) 中心问题为:
输入:完全图 \(G=(V,E)\),边带正权,且满足三角不等式 \(w_{uv} \le w_{uk} + w_{kv}\),以及一个正整数 \(k\)。
目标:求一个点集 \(|S|=k\)(称为 \(k\) 个中心),定义一个点到一个点集的距离 \[ d(u,S) = \min_{v\in S} w_{uv} \] (显然,如果满足三角不等式,那么任意两点之间的最短距离就是直接连接两点的边权)
要求最小化 \(\max_{u\in V} d(u,S)\)。即所有顶点到这 \(k\) 个中心的最短路程的最大值(不妨称之为这个这个 \(k\) 中心的代价)最小。
近似算法 1(Gonzalez)
算法
- 任意选取一个顶点并将其加入 \(S\)。
- 选取离当前 \(S\) 最远的顶点加入 \(S\)。
- 重复步骤 2 直至 \(|S|=k\)。
第 2 步的操作是非常合乎直觉的:如果不把离 \(S\) 最远的顶点加入 \(S\) 的话,这条最远的边权就可能会被计入答案当中,这显然是不合算的,而如果将这个最远点作为新的中心,那么这条最远边就必定不会被计入答案。
分析
这个算法给出方案的代价是什么?在这个算法的背景下,我们不妨说:这个算法结果的代价是如果不跳出循环,下一个选取的中心到当前 \(S\) 的距离(依据第 2 步)。假设这个中心为 \(x\),我们不妨画图:
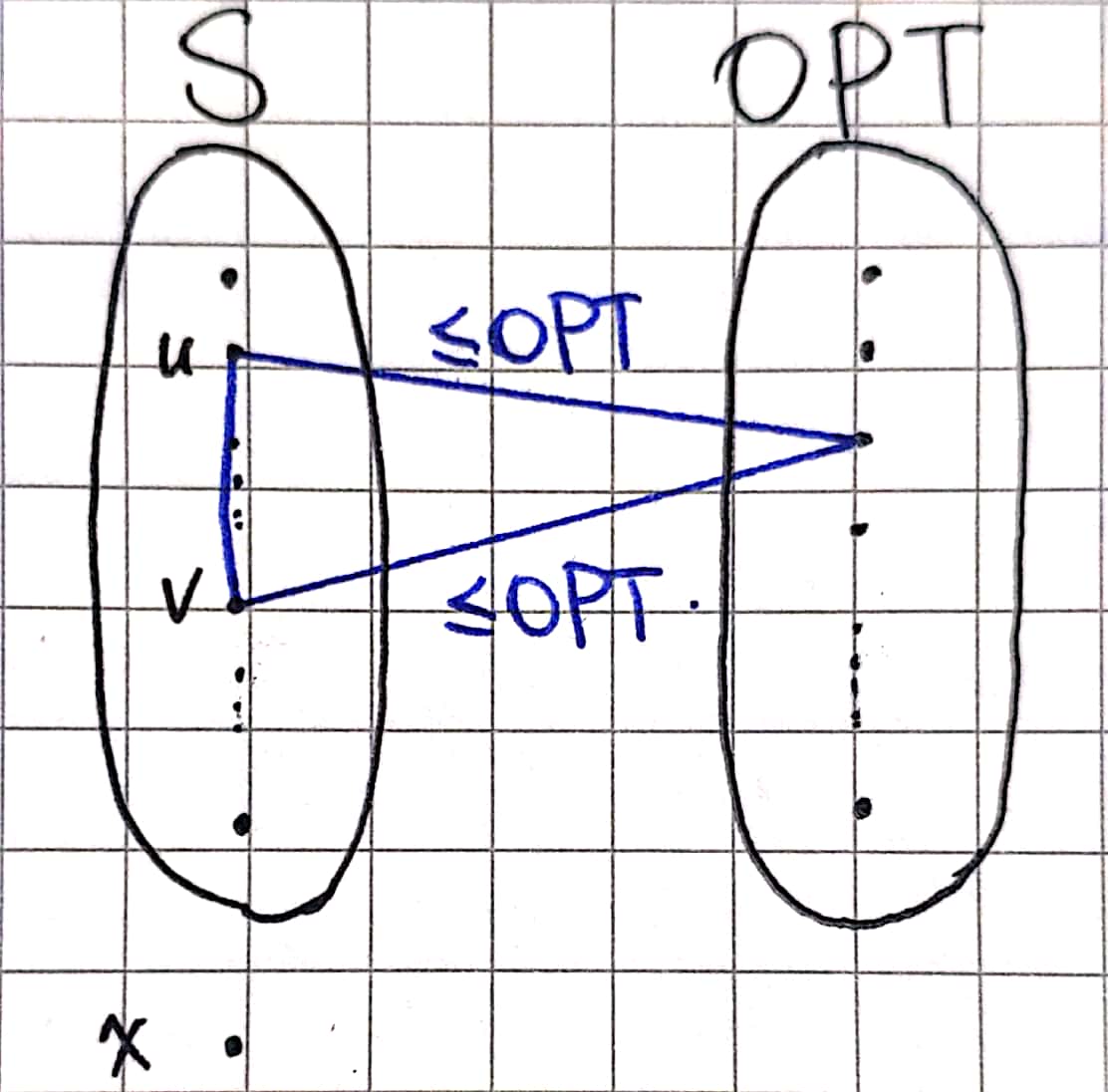
其中左边的 \(S\) 是我们的解,右边是最优解(我们这里把他们化成了不重叠的形式,事实上有重叠对于我们的论证也不造成影响)。
我们的解加上 \(x\) 总共有 \(k+1\) 个点,最优解有 \(k\) 个点,因此由抽屉原理,至少左边有两个点,它们在最优解中的最近点是相同的(即图中的两条横叉边),且由于是最优解,两条边的长度都 \(\le \mathrm{OPT}\)。
不妨设这两个点为 \(u,v\),由三角不等式,可以得出 \(w_{uv}\le2\cdot\mathrm{OPT}\)。
接下来不妨假设 \(u,v\) 中的后来者为 \(v\),为什么当时我们选择 \(v\) 而不是 \(x\) 加入 \(S\) 呢?肯定是因为当时 \(d(v,S)\ge d(x,S)\)。而由 \(d(v,S)\) 的定义可知,\(d(v,S)\le w_{uv}\),且由于随着 \(S\) 的变大,\(d(x,S)\) 不增,因此我们解的代价(即现在的 \(d(x,S)\))一定也是不大于当时的 \(d(v,S)\)。将这些不等式串联起来,便得到: \[ d(x,S) \le w_{uv} \le 2\cdot \mathrm{OPT} \] 也就是说这个算法的近似比为 \(2\)。
近似算法 2(Hochbaum & Shmoys)
算法
我们不妨假设我们已经知道了最优解的代价 \(\mathrm{OPT}\),那么我们要怎么做呢?
- 我们选取任意顶点 \(u_1\) 加入中心,并以为中心画一个半径为的球,钦定球内的所有点归 \(u_1\)。
- 我们接着选取一个在这个球以外的一个顶点 \(u_2\) 加入中心,并以 \(u_2\) 为中心画一个半径为 \(2\cdot \mathrm{OPT}\) 的球,钦定球里面的点归 \(u_2\)。
- 我们接着选取一个在 \(u_1\) 和 \(u_2\) 的球外的点 \(u_3\) 作为中心……
- 重复上述步骤,直至图上的所有点都归一个至多 \(2\cdot \mathrm{OPT}\) 远处的中心管。
画在图上大概是这样的:
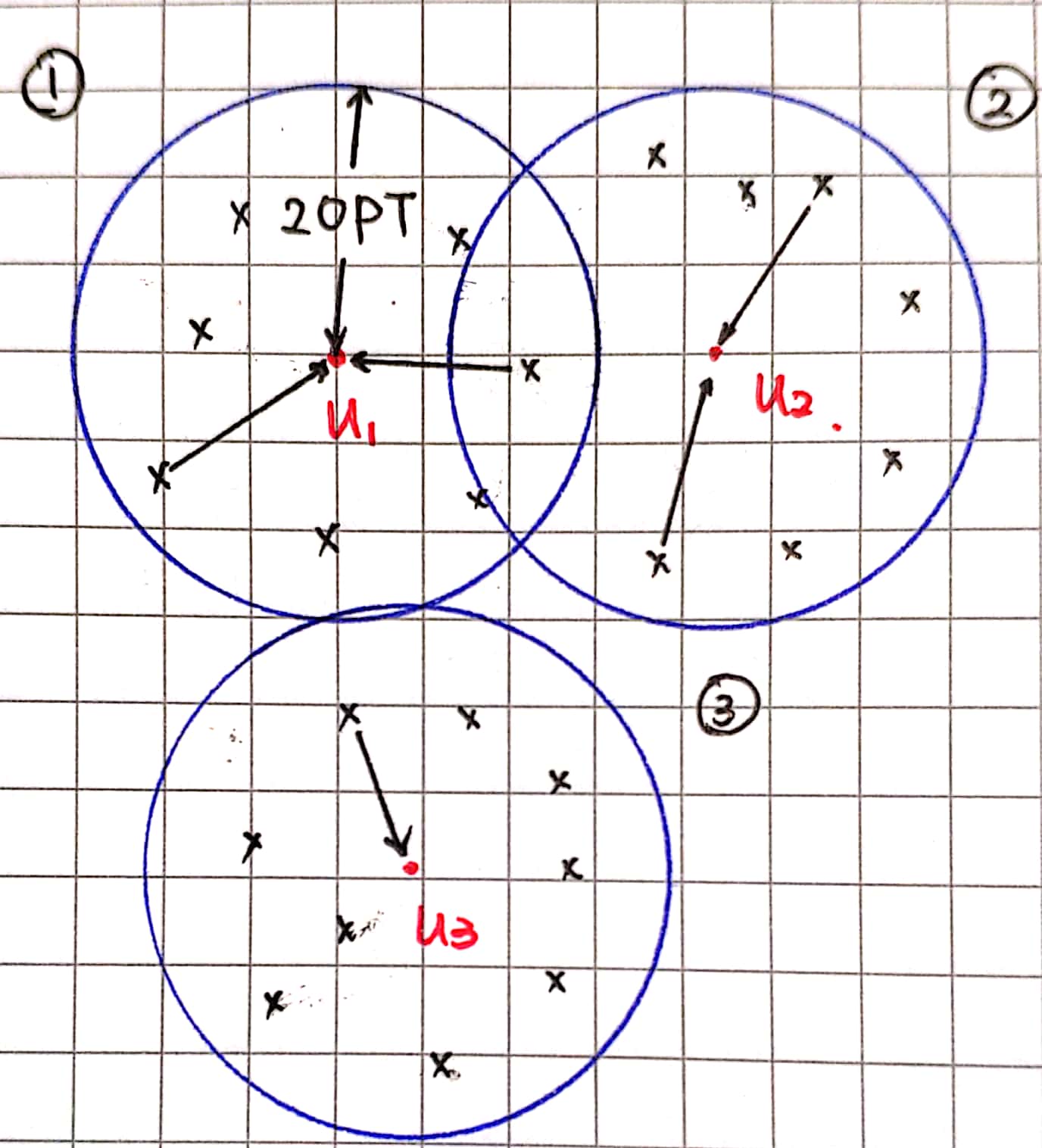
可以看到,可能会有点同时处在多个中心的 “势力范围” 之内,但这并不重要,我们只需要确保每个点离最近的一个中心至多 \(2\cdot \mathrm{OPT}\) 那么远就行了。
分析
我们接下来证明这是一个 \(2\) 近似算法。算法本身的流程确保了 \(2\) 的近似比,因此唯一需要证明的就是这个算法产生的中心不超过要求的 \(k\) 个。
不妨反证:如果产生了超过 \(k\) 个中心呢?
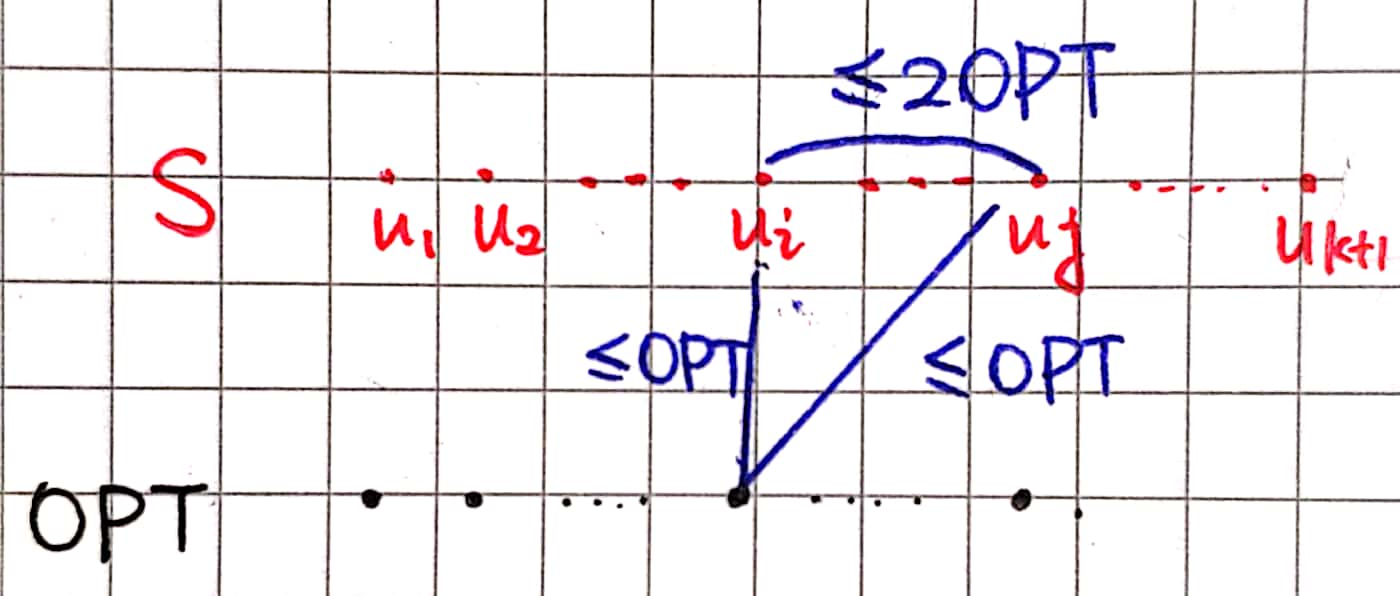
那么根据抽屉原理,至少有两个中心在最优解中的最近点是相同的(这和我们分析第一个算法时的逻辑是完全相同的),由三角不等式,这两个中心之间的距离 \(\le 2\cdot \mathrm{OPT}\)。但是根据算法,中心之间两两距离应该大于 \(2\cdot \mathrm{OPT}\),这就产生了矛盾。
因此必定不会有超过 \(k\) 个中心,证毕。
还剩下来一个问题:这个算法假定我们知道 \(\mathrm{OPT}\),但是实际上我们不知道啊!
但是我们知道 \(\mathrm{OPT}\) 一定是某一条边的边权,因此我们只需要按边权从小到大枚举每一条边,把边权当做 \(\mathrm{OPT}\) 试试看,如果产生超过 \(k\) 个中心那必然不是 \(\mathrm{OPT}\)(这是我们推论的逆否),而反之则可能就是 \(\mathrm{OPT}\)(但无论如何,事实上是 \(\mathrm{OPT}\) 的那条边一定是没有问题的)。因为我们在这里只在意是否是多项式时间复杂度而不在意复杂度本身,而枚举边自然是多项式时间的,因此没有任何问题(当然,在实现过程中可以考虑使用二分,但这就是后话了)。
近似比可以更好吗?
定理:如果存在一个多项式时间的,近似比 \(<2\) 的 \(k\) 中心问题的近似算法,那么 \(\mathsf{P}=\mathsf{NP}\)。
证明:考虑最小支配集问题的判定形式:
输入:无向图 \(G=(V,E)\) 以及正整数 \(k\)。
判定:是否存在一个大小为 \(k\) 的支配集?支配集定义为一个点集 \(S\subseteq V\),使得 \(\forall u\in V\),要么 \(u\in S\) 或者 \(u\) 的邻居 \(\in S\)。
最小支配集问题是 NPC 的。我们接下来将其规约到 \(k\) 中心问题(也是判定形式):
输入:完全图 \(G'\),正整数 \(k,b\)。
判定:是否存在一个代价 \(\le b\) 的 \(k\) 中心的方案?
如何规约?不难想到,我们可以让 \(G\) 与 \(G'\) 用相同的点集,而对于所有在 \(G\) 中的边,其在 \(G'\) 中的边权为 \(1\)。而对于所有不在 \(G\) 中的边,其在 \(G'\) 中的边权为 \(2\)(为什么是 \(2\)?直觉上我们会首先想到 \(\infty\),但是这样就不满足三角不等式了,因此改成 \(2\))。令两个问题当中的 \(k\) 相等,且 \(b=1\),我们就完成了规约。
为什么?
在这样的规约下,一个在 \(G\) 中的支配集必然对应一个 \(G'\) 当中代价为 \(1\) 的相同大小的 \(k\) 中心,反之亦然。
也就是说,如果我们可以解决这个规约后的 \(k\) 中心问题,那么我们就能解决原来的最小支配集问题了。
这个时候就可以看出为什么近似比 \(<2\) 的近似算法牛逼了:
- 如果 \(G\) 当中有符合要求的支配集,那么 \(k\) 中心的 \(\mathrm{OPT}=1\),而由于近似比 \(<2\) 且边权只有 \(1,2\),因此即使是近似算法也会次次给出 \(1\)。
- 如果 \(G\) 当中没有符合要求的支配集,那么 \(k\) 中心的 \(\mathrm{OPT} = 2\),而由于近似比 \(<2\) 且边权只有 \(1,2\),因此即使是近似算法也只能给出 \(2\)。
如此说来,即使是近似算法,通过判断输出代价是 \(1\) 还是 \(2\) 我们就能判断 \(G\) 中有没有大小 \(k\) 的支配集。而这个近似算法是多项式时间的,因此我们可以用多项式时间解决支配集问题这么一个 NPC 问题,即 \(P=NP\)。
刚刚用到的这个技巧被称为 “gap reduction”。
整个定理的言下之意就是如果你也相信 \(\mathsf{P}\neq \mathsf{NP}\),那么就可以洗洗睡了~