概率论初步
期望的线性性
\[ \mathbb{E}[X+Y] = \mathbb E [X] + \mathbb E[Y] \]
随机变量的方差
\[ \begin{aligned} \operatorname{Var}[X] &:= \mathbb{E}\left[\left(X-\mathbb{E}[X]\right)^2\right] \\ &= \mathbb{E} \left[X^2 - 2\mathbb{E}[X]X+\mathbb{E}[X]^2\right] \\ &= \mathbb{E} \left[X^2\right] - 2\mathbb{E}[X]^2 + \mathbb{E}[X]^2 \\ &= \mathbb{E} \left[X^2\right] - \mathbb{E}[X]^2 \end{aligned} \]
推论:若随机变量 \(X,Y\) 互相独立,则有:
- \(\operatorname{Var}[X+Y] = \operatorname{Var}[X] + \operatorname{Var}[Y]\)
- \(\mathbb{E}[XY] = \mathbb{E}[X]\mathbb{E}[Y]\)
(互相独立的定义:\(\forall x, y, \operatorname{Pr}[X=x\cap Y=y]=\operatorname{Pr}[X=x]\operatorname{Pr}[Y=y]\))
马尔科夫不等式
设 \(X\) 为非负随机变量,则 \(\forall a >0\): \[ \operatorname{Pr}[X\ge a] \le \frac{\mathbb{E}[X]}{a} \] 证明: \[ \begin{aligned} \mathbb{E}[X] &= \sum_{x}x\operatorname{Pr}[X=x] \\ &= \sum_{x<a}x\operatorname{Pr}[X=x] + \sum_{x\ge a}x\operatorname{Pr}[X=x] \\ &\ge \sum_{x\ge a}x\operatorname{Pr}[X=x] \\ &\ge \sum_{x\ge a}a\operatorname{Pr}[X=x] \\ &= a \sum_{x\ge a}\operatorname{Pr}[X=x] \\ &= a \operatorname{Pr}[X\ge x] \end{aligned} \] (离散形式,连续形式的证明方法类似)
其中第一个 \(\ge\) 依赖于 \(X\) 非负的特性,因此非负是必须的!
马尔科夫不等式让我们可以在只知道随机变量期望的情况下对于其分布概率进行粗略定界。
切比雪夫不等式
设 \(X\) 为随机变量,则 \(\forall a > 0\): \[ \operatorname{Pr}\left[|X-\mathbb{E}[X]| \ge a\right] \le \frac{\operatorname{Var}[X]}{a^2} \] 证明: \[ \begin{aligned} \operatorname{Pr}\left[|X-\mathbb{E}[X]| \ge a\right] &= \operatorname{Pr}\left[(X-\mathbb{E}[X])^2 \ge a^2\right] \\ &\le \frac{\mathbb{E}\left[(X-\mathbb{E}[X])^2\right]}{a^2} \\ &= \frac{\operatorname{Var}[X]}{a^2} \end{aligned} \] 注意到 \(a^2>0\) 且 \((X-\mathbb{E}[X])^2\) 非负,因此我们可以在第二步使用马尔科夫不等式。
如果我们不仅知道随机变量的期望(一阶矩),还知道其方差(二阶矩),那么切比雪夫不等式可以给出比马尔科夫不等式更为精确的上界。
切尔诺夫上界(Chernoff Bound)
设随机变量 \(X=\sum_{i=1}^n X_i\),其中 \(X_1,\cdots,X_n\) 为 \([0,1]\) 上互相独立的随机变量,则 \(\forall t>1\): \[ \operatorname{Pr}\left[|X - \mathbb{E}[X]| \ge t\mathbb{E}[X]\right] \le 2\exp\left(-\frac{t\mathbb{E}[X]}{3}\right) \] 且 \(\forall \epsilon \in (0,1]\): \[ \operatorname{Pr}\left[|X - \mathbb{E}[X]| \ge \epsilon\mathbb{E}[X]\right] \le 2\exp\left(-\frac{\epsilon^2\mathbb{E}[X]}{3}\right) \] 加性切尔诺夫不等式(Additive Chernoff Bound):\(\forall b >1\): \[ \operatorname{Pr}\left[|X - \mathbb{E}[X]| \ge b\right] \le 2\exp\left(-\frac{2b^2}{n}\right) \]
三个不等式给出上界的比较
考虑如下问题:投 \(n\) 次均质硬币,设随机变量 \(X\) 表示头朝上的次数。估计 \(\operatorname{Pr}\left[X\ge \frac{3n}{4}\right]\)?
马尔科夫不等式:
显然,\(\mathbb{E}[X]=\frac{n}{2}\),且 \(X\) 非负: \[ \operatorname{Pr}\left[X\ge \frac{3n}{4}\right] \le \frac{\frac{n}{2}}{\frac{3n}{4}} = \frac{2}{3} \] 这个上界是很松的。
切比雪夫不等式:
设随机二元变量 \(X_i\) 表示第 \(i\) 次投是否头朝上,则显然 \(X=\sum_{i=1}^nX_i\),且易得 \(\operatorname{Var}[X_i]=\frac{1}{4}\),由于 \(X_i\) 两两独立,则 \(\operatorname{Var}[X]=\frac{n}{4}\),运用切比雪夫不等式: \[ \begin{aligned} \operatorname{Pr}\left[X\ge \frac{3n}{4}\right] &= \operatorname{Pr}\left[X - \frac{n}{2}\ge \frac{n}{4}\right] \\ &= \frac{1}{2}\operatorname{Pr}\left[\left|X - \frac{n}{2}\right|\ge \frac{n}{4}\right] \\ &= \frac{1}{2}\operatorname{Pr}\left[\left|X - \mathbb{E}[X]\right|\ge \frac{n}{4}\right] \\ &\le \frac{1}{2} \frac{\frac{n}{4}}{\left(\frac{n}{4}\right)^2} \\ &= \frac{2}{n} \end{aligned} \] 切尔诺夫上界:
显然,取 \(\epsilon = \frac{1}{2}\): \[ \begin{aligned} \operatorname{Pr}\left[X\ge \frac{3n}{4}\right] &= \operatorname{Pr}\left[X - \frac{n}{2}\ge \frac{n}{4}\right] \\ &= \frac{1}{2}\operatorname{Pr}\left[\left|X - \frac{n}{2}\right|\ge \frac{n}{4}\right] \\ &= \frac{1}{2}\operatorname{Pr}\left[\left|X - \mathbb{E}[X]\right|\ge \frac{1}{2}\mathbb{E}[X]\right] \\ &\le \exp\left(-\frac{1}{12}\cdot \frac{n}{2}\right)\\ &= \exp\left(-\frac{n}{24}\right) \end{aligned} \] 各上界的效果:
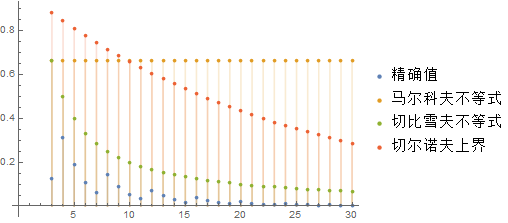
看来这个例子里面还是切比雪夫不等式给出的上界最好 —— 是不是切尔诺夫上界我学到的形式本身太 loose 了?
近似算法初步
定义
若算法 \(A\) 满足以下条件,则称算法 \(A\) 是某个问题(不妨假设是最小化问题)的 \(\alpha\) 近似比的近似算法:
- \(A\) 是多项式时间的。
- 对于所有输入,\(A\) 的输出 \(\operatorname{soln}(A) \le \alpha \cdot\mathrm{OPT}\),其中 \(\mathrm{OPT}\) 是该输入的最优解。
对于最大化问题,第二个条件为 \(\operatorname{soln}(A) \ge \frac{1}{\alpha} \cdot\mathrm{OPT}\)。
(继续假设是最小化问题)
显然,为了精确计算 \(\alpha\) 我们必须知道 \(\mathrm{OPT}\),而这显然是不现实的(如果可以我还要近似算法干嘛?),因此我们退而求其次寻找 \(\mathrm{OPT}\) 的一个比较紧的下界,我们的解与该下界之比自然就是 \(\alpha\) 的上界了。
例:最小顶点覆盖问题
输入:\(G=(V,E)\)
目标:最小化点集 \(S\subseteq V\),同时满足 \(\forall (u,v) \in E\),\(u\in S\) 或 \(v \in S\)。
这是一个知名的 NP Complete 问题。在这里我们设计一个简单的 \(2\) 近似算法。然而令人吃惊地是,\(2\) 的近似比已经是我们目前能够做到的最好结果!
思路:考虑 \(G\) 的一个极大匹配,显然极大匹配是可以在多项式时间内求出的。
同时注意到,任意无向图极大匹配的大小必定是其点覆盖集大小的下界,因为点覆盖必须取极大匹配当中每一条边的至少一个端点才能完成覆盖!
算法:
- 计算 \(G\) 的一个极大匹配 \(M\)。
- 取极大匹配所有边的所有端点为 \(S\)。
为什么正确?考虑反证:若 \(\exists (u,v) \in E\),使 \(u\not\in S\) 且 \(v \not \in S\),那显然边 \((u, v)\) 还可以加入 \(M\),这和 \(M\) 的极大性是矛盾的。
近似比证明: \[ \begin{aligned} |S| = 2|M| \le 2\cdot \mathrm{OPT} \end{aligned} \] 得证。