The enemy knows the system. ——Claude Shannon

闷声大发财，这是坠吼的！ ——?

程序是一个月以前写的。决定重新启用博客之后就把想法心得写一写吧，顺便把灵敏度分析补上。

OI 的奇怪知识点可真多～

什么是 SOCKS5?

SOCKS5 是 RFC1928 定义的一类网络代理协议。

理论上来说，由于其简洁性，理论上 SOCKS5 是开销最低的代理协议。

然而由于其过于简单，数据可以明文传输的特点，其流量特征非常明显，容易被干扰。因此在某些地区从很久以前就不能有效使用了。

话虽如此，由于其协议简单，用作学习用途真是极好的。

什么是 NTT?

NTT 是离散傅里叶变换在 \(\mathbb{Z}/p\mathbb{Z}\)（其中 \(p\) 是素数）上的推广。

具体的 NTT 以及 FFT 算法可以看之前的笔记 NTT 笔记。

协议设计

因为一个字节是 8 个比特，我们使用 \(\mathbb{Z}/257\mathbb{Z}\) 下长度为 \(256\) 的序列 NTT。

但是 \(\mathbb{Z}/257\mathbb{Z}\) 毕竟不是 \(\mathbb{Z}/256\mathbb{Z}\)，如果尝试把 \(256\) 放进字节里面就会溢出。考虑到这一点，定义如下的协议结构来储存 NTT 的结果。

意义:	溢出数	溢出下标	NTT 序列模 \(256\)
字节数:	1	溢出数	256

对于一段数据流，我们一次至多取 \(255\) 字节，把这一段的长度放在最前面组成共 \(256\) 个字节的数据块，NTT 之后在放到上面这张表当中拼成至少 \(257\) 字节的数据块。（理论上可以通过 Padding 省掉储存长度的字节）

解码类似，先从上表规定的数据块复原出 NTT 序列，然后再 INTT 以下获得原序列，就行了。

由于被 NTT 过的数据特征已经和明文的数据特征大不一样，因此可以规避一些现有的检测。

但是根据本文一开头的 Shannon’s Maxim（又称 Kerckhoff Principle），NTT 无疑会带来新的数据特征，因而其 obscurity 源于对方对使用了 NTT 这一事实本身的不知晓或忽视，这和加密还是不一样的。

实现

这种网络应用程序果然还是应该用 Go 写啊～

你看这 goroutine，它不香吗？

因为 NTT 是成块处理的，无论是在写还是在读的时候都需要额外的 buffer 来缓存长度不够的块，就这一部分需要一点细节，总体按照上述协议实现一个套 NTT 的 ReadWriter 还是很简单的。写好的 NTTReadWriter 不仅可以套在 Conn 上，还可以套在文件上实现文件 NTT 之类的（虽然似乎没啥卵用）。

在网络方面，客户端就留一个 relay 把本地监听的 SOCKS 请求 NTT 之后 forward 到服务端，然后服务端处理请求之后再 forward 回去就行了。用 goroutine 写这些还是很容易的。

最后要在服务端实现 SOCKS 协议，这个似乎 Go 没有现成库的样子（现成的都很难和 NTT 耦合），于是只能自己写。最后的成品支持 RFC1928 中规定的 Connect 和 Bind 请求，功能基本上全了。

在性能方面，我写的 NTTReadWriter 本身的性能测试下来应该在 \(30\mathrm{MB/s}\) 左右，虽然不高但是已经超过网速了。最后在 VPS 上的综合测试结果也是能够跑满网速，8K 不卡，非常顺滑。

代码？不存在的。

优缺点

优点

把 NTT 用在网络通讯上的骚操作似乎我还没有听说过。（或许是我见识粗鄙了）
NTT 对于微小的扰动很敏感，因此数据特征应该会出现很大的变化。（会在下一个部分展示）
NTT 因为使用了大量的模运算，计算的开销比较大，块大小也不小。这对许多基于流模型的检测方法提出了挑战。

缺点

太慢了。（虽然也足以跑满带宽）
一般来说一个 NTT 块至多只有两个溢出，也就表明数据流中平均每 \(256-258\) 个字节就会有一个很小的数，这不失为一个比较明显的特征。
溢出位的记录导致额外的流量开销。（大概在 \(1\%\) 的水平，还是相当可以接受的）

灵敏度分析

直觉告诉我 NTT 对于源数据的微小变化应该是非常敏感的，就算是一点点微扰在一层层处理之后也会让最后的结果面目全非。这也是我开脑洞选择用 NTT 隐藏 SOCKS 特征的原因（而且事实就是成功了（喜））。

但是直觉总是不靠谱的。还是需要具体数据。

测试环境如下：

# 这似乎不是最 Pythonic 的写法（悲）
import numpy as np
import matplotlib.pyplot as plt

MOD = 257
G = 3
LOG = 8
LEN = 1 << LOG

def qpow(x, y):
    ret = 1
    while y != 0:
        if y & 1 == 1:
            ret = ret * x % MOD
        x = x * x % MOD
        y >>= 1
    return ret

pos = np.zeros(LEN, dtype=int)
for i in range(1, LEN):
    pos[i] = ((i & 1) << (LOG - 1)) | (pos[i >> 1] >> 1)
    
def ntt(x, d=1):
    y = np.array([x[pos[i]] for i in range(LEN)])
    for k in range(LOG):
        half, span = 1 << k, 1 << (k + 1)
        w_ = qpow(G, (MOD - 1) // span)
        if d == -1:
            w_ = qpow(w_, MOD - 2)
        for l in range(0, LEN, span):
            mid = l + half
            w = 1
            for i in range(half):
                t = w * y[mid + i] % MOD
                y[mid + i] = (y[l + i] - t) % MOD
                y[l + i] = (y[l + i] + t) % MOD
                w = w * w_ % MOD
    return qpow(LEN, MOD - 2) * y % MOD if d == -1 else y

不同位置，相同扰动

x = np.random.randint(MOD, size=LEN)
ys = []
for i in range(LEN):
    x_ = np.copy(x)
    x_[i] = (x_[i] + 1) % MOD
    ys.append(ntt(x_))
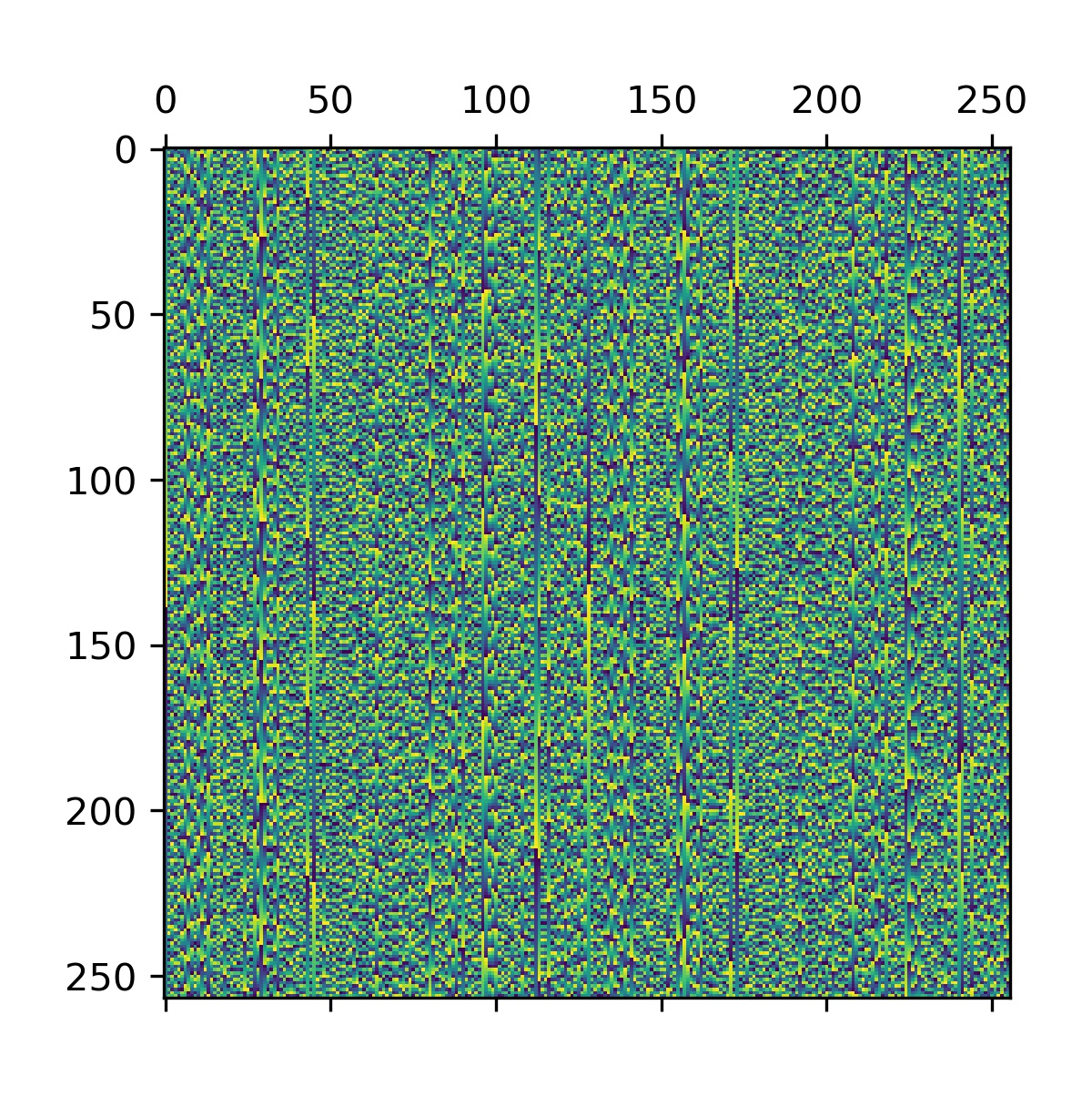
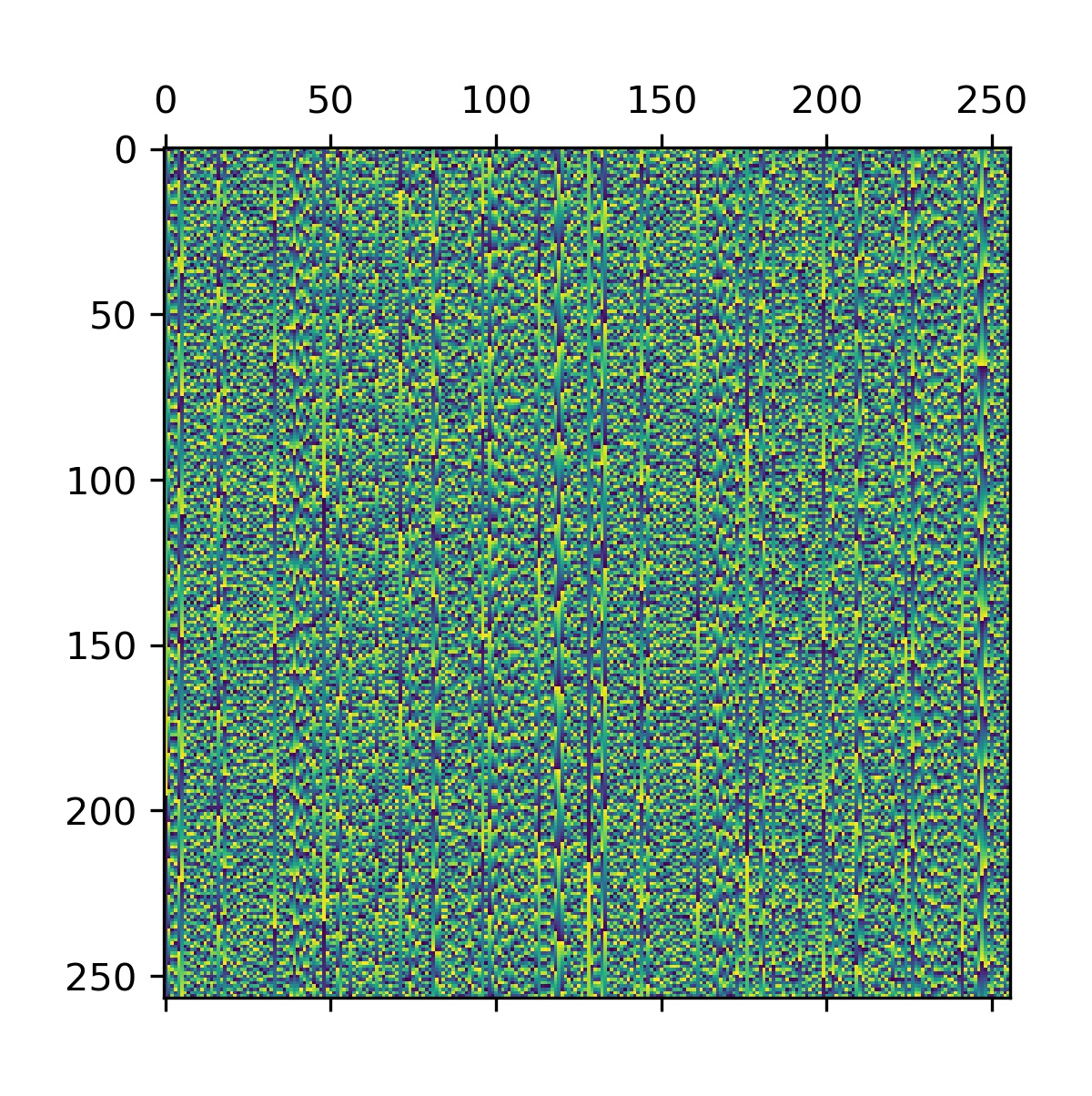
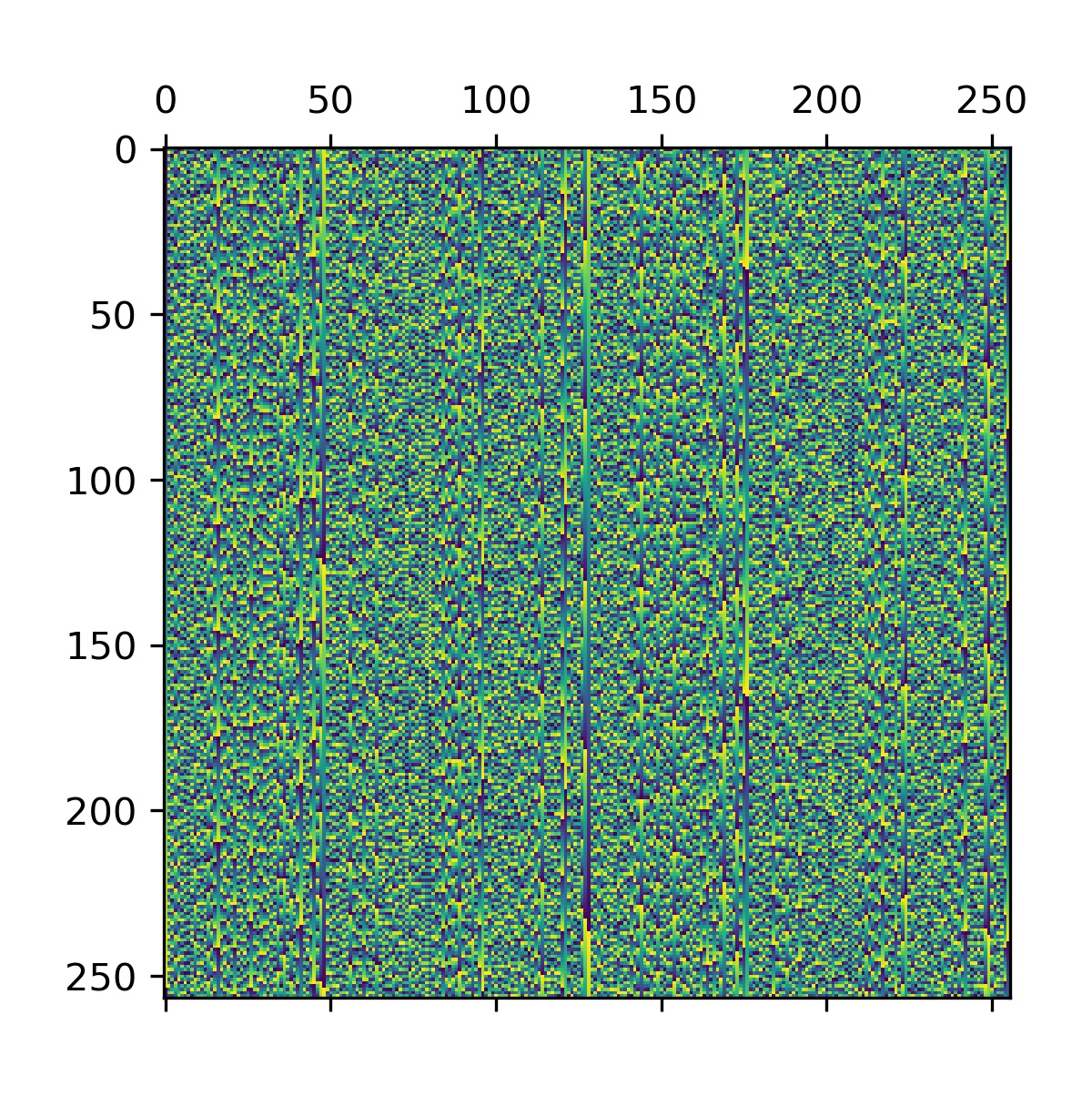
plt.matshow(np.array(ys))

即测试在原数列不同位置加 \(1\) 微扰后对于 NTT 后数列的影响。结果如下：

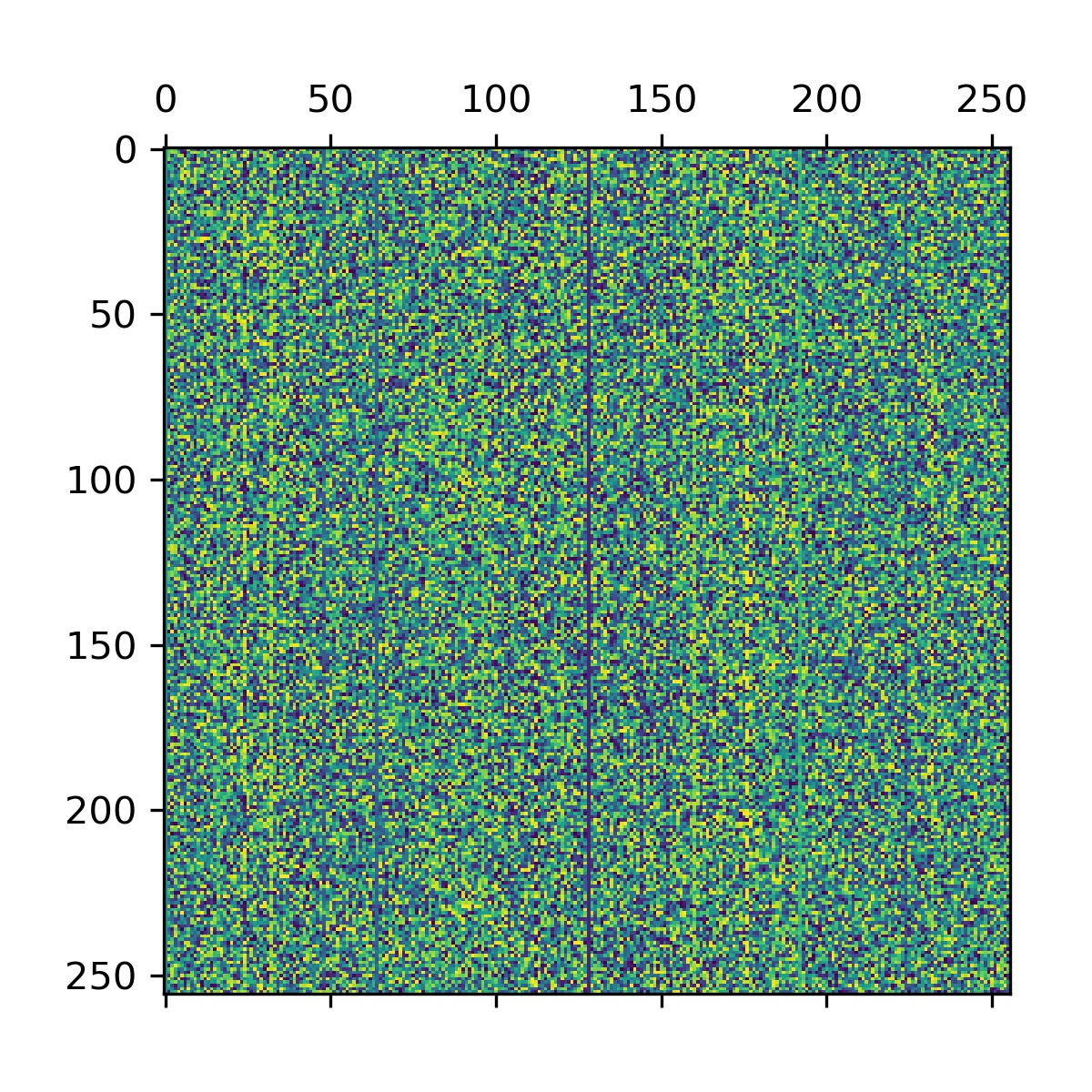
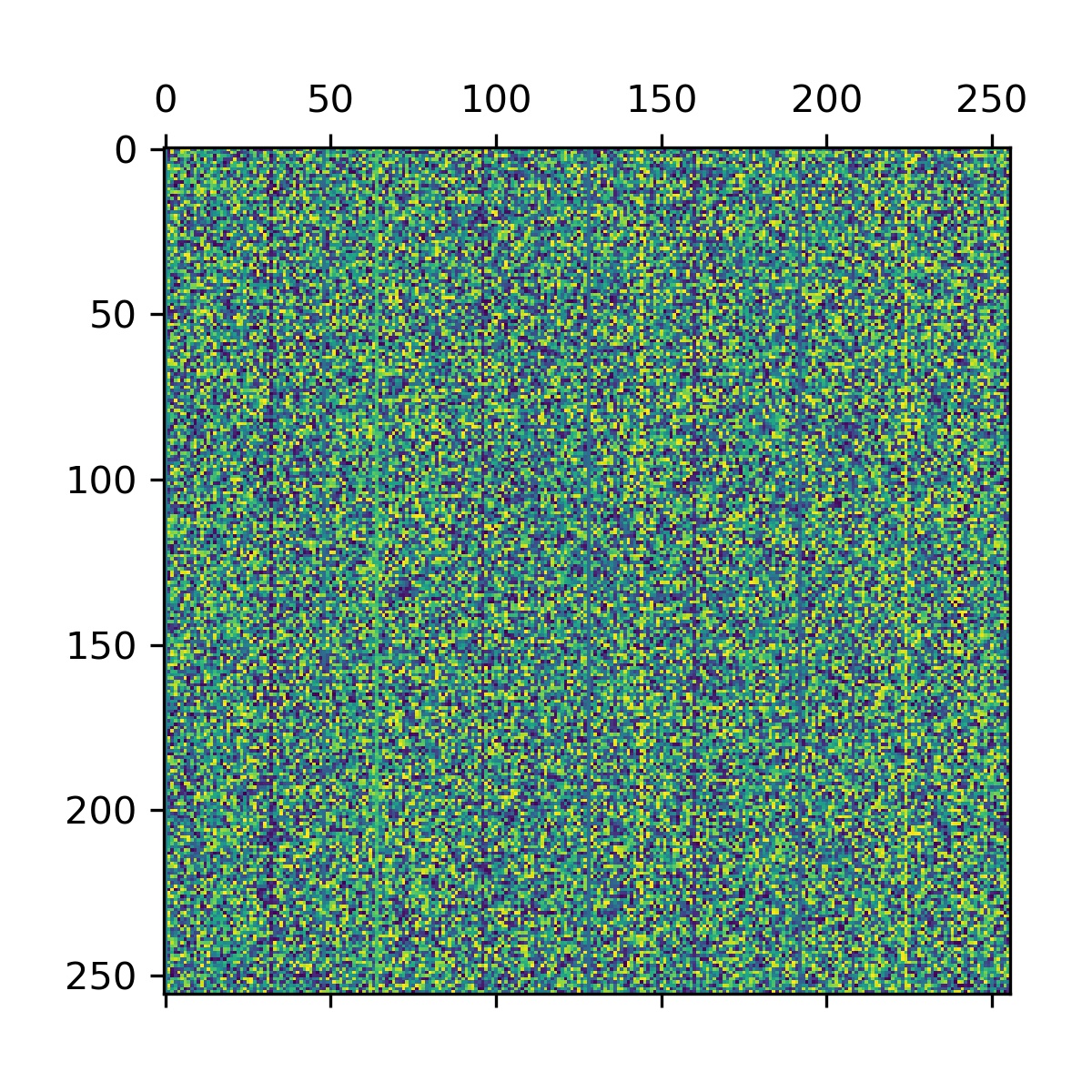
除了位置（例如中间，大概是直流分量？）看起来都还不错！

同一位置，不同扰动

x = np.random.randint(MOD, size=LEN)
p = np.random.randint(LEN)
ys = []
for i in range(LEN):
    x_ = np.copy(x)
    x_[p] = (x_[p] + i) % MOD
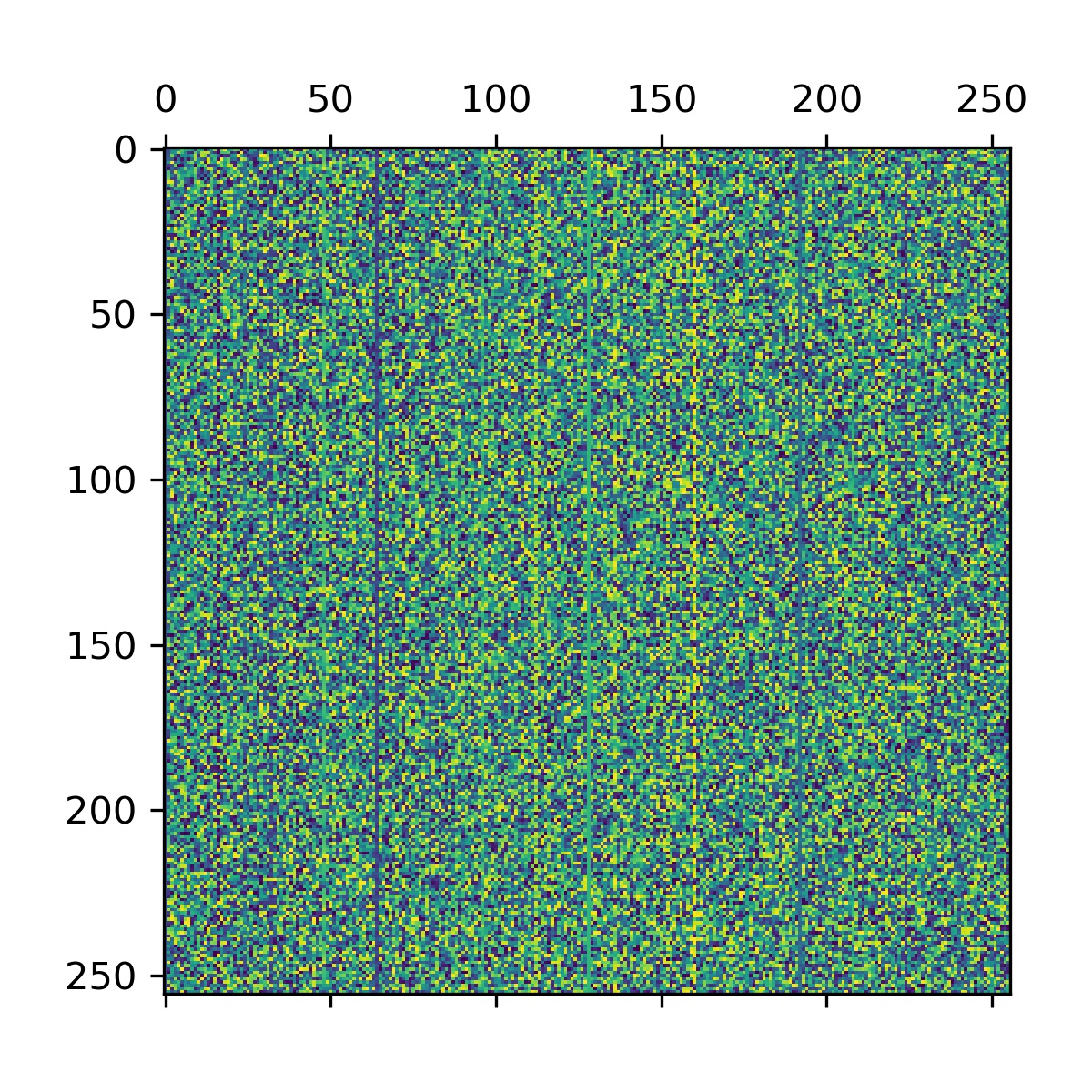
    ys.append(ntt(x_))
plt.matshow(np.array(ys))

即测试在原数据相同位置施加不同扰动对于 NTT 结果的影响，结果也还不错：

NTT 在 SOCKS5 代理中的奇妙应用

Table of Contents