Intro
Redstone has been a core element in the game Minecraft for quite some years. It is presumably the most untrivial one as well: while anyone could master nearly all Minecraft mechanics through experiences, it takes not only experience but also ingenuity to design a good redstone circuit. Few of us are bold enough to claim “I master redstone”, even after playing Minecraft for a decade.
So here comes the question: Can the design of redstone circuits, the core of Minecraft automations, be automated? and If so, how? (appreciate how meta this is :)
Theoretically, the answer is “yes…but”. Minecraft has a finite world, and each position has a finite number of possible blockstates. We can write a program to enumerate all possible placements of blocks until we find some placement corresponding to the desired redstone circuit. However, this needs exponential time and we may need to wait for a century before it could give us, for instance, a decent piston door. Moreover, if a circuit involves manipulation of entities (which could have infinite many states), then we are easily screwed.
Well, perhaps it is difficult to let a program design any redstone circuit. But there is indeed a subset of redstone circuits whose design can very likely be automated—computational redstone circuits, aka. logic gates, calculators, CPUs etc. Why? Because software that design their real world electronic counterparts are readily available, i.e. EDA software.
As a high school student I, of course, know little about the inner workings of real-world EDA applications (and there doesn’t seem to be a lot of resources out there). I am convinced that this problem is NPC (further articulated below), so designing an efficient polytime combinatorial algorithm doesn’t seem plausible. That said, what about reducing this problem to some other NPC problems which we can solve relatively quickly with optimized algorithms / heuristics—say, ILP? This is what I am trying to do here.
Formulating the problem
“Designing computational redstone circuit automatically” is a vague idea, so it is necessary that we know what this truly means.
What’s the input?
The input should describe the intended functionality of a circuit. Recall how we usually describe a circuit: we draw a circuit diagram. I here characterize a redstone circuit diagram by the assumptions and constraints below:
- A circuit contains two parts: wires and components.
- Components are the primitives of a circuit. E.g. A torch or a wire junction.
- A component has interfaces, either in or out, as where the component receives signals from and sends signals to.
- A wire connects an out-interface from a component (“source”) to an in-interface of another component (“target”).
- Wires are directed.
- Components are independent. i.e. they do not interfere with other components in any way other than being connected by wires from interfaces.
A circuit diagram can be represented in a directed graph, with components as vertices and wires as edges. Source/target interfaces as extra information stored on edges.
What’s the output?
We want our program to tell us how the circuit we described in the input can be built in the Minecraft world. Therefore, we could define the the output to be a set of position - blockstate pairs, (which, in implementation, can be stored in a schematic file).
However, we don’t want to jump straight from a circuit diagram to a detailed Minecraft schematic because that means taking interference between components, quasi connectivity, update order—basically everything that makes redstone engineering complex—into consideration in the first place.
Instead, we could first build our circuit in an ideal world, in which we forget about all those factors above, and then convert the ideal placement into an actual Minecraft schematic.
What’s an idea world?
- A circuit consists of multiple ideal blocks.
- A component fully occupies a set of ideal blocks, some of which are its interfaces. How many and which blocks a certain type of component occupies depend on its size in Minecraft and how we plan to convert the ideal placement to a real schematic.
- A wire is a chain of ideal blocks, where any adjacent two share a face. The first block is always the source interface and the last is always the target interface.
- Exclusiveness: All components and all wires (ignoring their first and last block) mustn’t overlap.
- Mutual Independence: Unless both blocks are occupied by the same component / wire, anything in two adjacent cells do not interfere with each other. To meet this constraint, we could say (rather conservatively) that an ideal block should map to \(3\times 2 \times 3\) Minecraft blocks.
- Wire junctions are special components and are exceptions to rule 2 and 3. A wire junction always have three interfaces (1 in & 2 outs, or 2 ins & 1 out). Multiple junctions can overlap and they can overlap with an interface of some component.
- There are times when we want to fix the location of some components in the input. These components are usually just placeholders that mark the position of IO. (We don’t want to produce a circuit with an unreachable input/output in the center of everything else, right?)
The Objective
- The circuit represented by the output must have the same functionality as described by the input circuit diagram.
- The delay of the circuit should be minimized.
Example: the AND gate
Let’s see how we design a simple AND gate.
Suppose the only primitive components we have are NOT gate (torch), wire junction, and IO placeholder. The circuit diagram of AND gate is:
Reduction to Integer Programming
Once the problem statement is clear, we can proceed to convert the problem into an integer programming. Let’s start by defining some notations. First, assume there are \(n\) components and \(m\) wires in a circuit.
The circuit we are designing obviously must meet some space constraints. Hence, let \(F \subset \mathbb{Z}^3\) be the set of all feasible ideal block coordinates.
Then we have different types of components, which can be placed with different orientations (at most 6). Some component may not be placed in a certain direction due to limitations in Minecraft mechanisms (such contraptions are often known as “directional”). Let \(D_i\) be the set of feasible orientations of the \(i\) th component.
For each component \(i\) and a feasible orientation \(d\in D_i\), let \(C_{i,d} \subset \mathbb{Z}^3\) be the set of ideal block coordinates this component occupies when placed in this direction. For convenience, let \((0,0,0)\) be a tight lower bound of the three components in this set. We assume that the shape of a component, after fixing its type and orientation, is translation-invariant.
It’s finally time to introduce some variables. Let binary variables \(x_{i,d,\mathbf{u}} (d\in D_i, \mathbf{u} \in F)\) denote whether the \(i\) th component is placed with orientation \(d\) at coordinate \(\mathbf{u}\).
Every component should be placed only once. This gives the constraint
\[ \sum_{d\in D_i}\sum_{\mathbf{p} \in F} x_{i,d,\mathbf{p}} = 1, \quad \forall i = 1,\cdots,n. \]
And components should not overlap! Consequently,
\[ \sum_{i=1}^n\sum_{d\in D_i}\sum_{\substack{\mathbf{c}\in C_{i,d} \\ \mathbf{p}-\mathbf{c} \in F}} x_{i,d,\mathbf{p}-\mathbf{c}} \le 1,\quad \forall \mathbf{p} \in F. \]
This constraint applies for each location \(\mathbf{p}\) in the feasible space. We enumerate all components and their possible placements that would occupy \(\mathbf{p}\), making sure that their corresponding variables sum to at most 1.
Now we consider wires. For convenience, let \(N(\mathbf{u})\) denote \(\mathbf{u}\)’s neighbors in \(F\), \(N(\mathbf{u})\le 6\).
Let binary variables \(y_{i,\mathbf{u}, \mathbf{v}}(\mathbf{v} \in N(\mathbf{u}))\) denote whether the \(i\) th wire has a segment from \(\mathbf{u}\) to \(\mathbf{v}\), and let \(a_i\) and \(b_i\) be the indices of the source and destination component of wire \(i\).
Furthermore, let \(\mathbf{a}_{i,d}(d\in D_{a_i})\) be the coordinate of the source interface relative to the source component’s (\(a_i\)) location when the source component of the \(i\) th wire is placed with orientation \(d\). Define \(\mathbf{b}_{i,d}(d\in D_{b_i})\) in a similar manner, denoting the coordinate of the destination interface relative to the destination component’s location.
With these notations, the constraint that enforces the connectivity of wires can be written as
\[ \sum_{\mathbf{v} \in N(\mathbf{u})} \left(y_{i,\mathbf{u}, \mathbf{v}} - y_{i,\mathbf{v}, \mathbf{u}}\right) = \sum_{\substack{d\in D_{a_i}\\ \mathbf{u} - \mathbf{a}_{i,d} \in F}} x_{a_i,d,\mathbf{u} - \mathbf{a}_{i,d}} - \sum_{\substack{d\in D_{b_i}\\ \mathbf{u} - \mathbf{b}_{i,d} \in F}} x_{b_i,d,\mathbf{u} - \mathbf{b}_{i,d}}, \quad \forall \mathbf{u}\in F, i=1,2,\cdots,m. \]
Check: If \(\mathbf{u}\) is the starting location of wire \(i\). both LHS and RHS are 1; If \(\mathbf{u}\) is the ending location of wire \(i\). both LHS and RHS are \(-1\); Otherwise both sides equal 0.
Meanwhile, given that a location is either occupied by a component or a wire but never both, and that any two wires shall not overlap, we have the following constraint
\[ 2\sum_{i=1}^n\sum_{d\in D_i}\sum_{\substack{\mathbf{c}\in C_{i,d} \\ \mathbf{p}-\mathbf{c} \in F}} x_{i,d,\mathbf{p}-\mathbf{c}} + \sum_{i=1}^m\sum_{\mathbf{v} \in N(\mathbf{p})} \left(y_{i,\mathbf{p}, \mathbf{v}} + y_{i,\mathbf{v}, \mathbf{p}}\right) \le 2,\quad \forall \mathbf{p} \in F. \]
The intuition: Usually if a wire (say, \(i\)) passes through \(\mathbf{p}\), \(\sum_{\mathbf{v} \in N(\mathbf{p})} y_{i,\mathbf{p}, \mathbf{v}} + y_{i,\mathbf{v}, \mathbf{p}} = 2\), so the RHS should be 2. At the same time, we expect that when some component has occupied \(\mathbf{p}\), no wires should occupy \(\mathbf{p}\) again. We then need to use indicator
\[ \sum_{i=1}^n\sum_{d\in D_i}\sum_{\substack{\mathbf{c}\in C_{i,d} \\ \mathbf{p}-\mathbf{c} \in F}} x_{i,d,\mathbf{p}-\mathbf{c}}, \]
which is at most 1 by our second constraint, so we give it a coefficient of 2 to balance it with the wire term.
The above constraint, however, isn’t quite right: Wires and components do over lap at the interface block. To fix this, we amend the constraint to
\[ 2\sum_{i=1}^n\sum_{d\in D_i}\sum_{\substack{\mathbf{c}\in C_{i,d} \\ \mathbf{p}-\mathbf{c} \in F}} x_{i,d,\mathbf{p}-\mathbf{c}} + \sum_{i=1}^m\sum_{\mathbf{v} \in N(\mathbf{p})} \left(y_{i,\mathbf{p}, \mathbf{v}} + y_{i,\mathbf{v}, \mathbf{p}}\right) \le 2 + \sum_{i=1}^m\left(\sum_{\substack{d\in D_{a_i}\\ \mathbf{p} - \mathbf{a}_{i,d} \in F}} x_{a_i,d,\mathbf{p} - \mathbf{a}_{i,d}} +\sum_{\substack{d\in D_{b_i}\\ \mathbf{p} - \mathbf{b}_{i,d} \in F}} x_{b_i,d,\mathbf{p} - \mathbf{b}_{i,d}} \right),\quad \forall \mathbf{p} \in F. \]
The complicated summation term on the right will be greater than 0 if \(\mathbf{p}\) is an interface block for some component and wire.
These are all the constraints that I had thought of. Together, the integer programming instance is
\[ \require{mathtools} \begin{aligned} \text{minimize}\ &\sum_{i=1}^m\sum_{\mathbf{u}\in F}\sum_{\mathbf{v}\in N(\mathbf{u})} y_{i, \mathbf{u}, \mathbf{v}}, \\ \text{subject to}\ &\sum_{d\in D_i}\sum_{\mathbf{p} \in F} x_{i,d,\mathbf{p}} = 1, &\forall i = 1,\cdots,n;\\ &\sum_{i=1}^n\sum_{d\in D_i}\sum_{\substack{\mathbf{c}\in C_{i,d} \\ \mathbf{p}-\mathbf{c} \in F}} x_{i,d,\mathbf{p}-\mathbf{c}} \le 1,&\forall \mathbf{p} \in F;\\ &\sum_{\mathclap{\mathbf{v} \in N(\mathbf{u})}} \left(y_{i,\mathbf{u}, \mathbf{v}} - y_{i,\mathbf{v}, \mathbf{u}}\right) = \sum_{\mathclap{\substack{d\in D_{a_i}\\ \mathbf{u} - \mathbf{a}_{i,d} \in F}}} x_{a_i,d,\mathbf{u} - \mathbf{a}_{i,d}} - \sum_{\mathclap{\substack{d\in D_{b_i}\\ \mathbf{u} - \mathbf{b}_{i,d} \in F}}} x_{b_i,d,\mathbf{u} - \mathbf{b}_{i,d}}, &\quad \forall \mathbf{u}\in F, i=1,\cdots,m;\\ &2\sum_{i=1}^n\sum_{d\in D_i}\sum_{\substack{\mathbf{c}\in C_{i,d} \\ \mathbf{p}-\mathbf{c} \in F}} x_{i,d,\mathbf{p}-\mathbf{c}} + \sum_{i=1}^m\sum_{\mathbf{v} \in N(\mathbf{p})} \left(y_{i,\mathbf{p}, \mathbf{v}} + y_{i,\mathbf{v}, \mathbf{p}}\right) \\ &\quad \le 2 + \sum_{i=1}^m\,\sum_{\mathclap{\substack{d\in D_{a_i}\\ \mathbf{p} - \mathbf{a}_{i,d} \in F}}} x_{a_i,d,\mathbf{p} - \mathbf{a}_{i,d}} +\sum_{i=1}^m\,\sum_{\mathclap{\substack{d\in D_{b_i}\\ \mathbf{p} - \mathbf{b}_{i,d} \in F}}} x_{b_i,d,\mathbf{p} - \mathbf{b}_{i,d}},& \forall \mathbf{p} \in F. \end{aligned} \]
The objective is simply the sum of all \(y\) variables because it denotes the total length of all wires, which we aim to minimize if we want the circuit to be compact.
Keep in mind, however, that these constraints are merely the necessary conditions of a valid circuit. Given the complexity of the constraints, it is difficult to reason if all circuit configurations conforming to these constraint are valid circuits. I suppose the best way to check is to write some code and see if it gives what we what.
Preliminary Experiments
I did some very rudimentary test of my ILP formulation above with the Gurobi solver and ~1kLoC of Kotlin. The goal was to route the simple circuit described below:
val in1 = ComponentNode(FixedLocation(Vec3(0, 0, 0)))
val in2 = ComponentNode(FixedLocation(Vec3(1, 0, 0)))
val out = ComponentNode(FixedLocation(Vec3(0, 0, 3)))
val a = ComponentNode(NotGate)
val b = ComponentNode(NotGate)
val c = ComponentNode(NotGate)
val d = ComponentNode(NotGate)
val e = ComponentNode(NotGate)
val circuit = MutableCircuitGraph()
// Connect the IO interface of in1 to the IN interface of a
circuit.addWire(in1, FixedLocation.IO, a, NotGate.IN)
circuit.addWire(in2, FixedLocation.IO, a, NotGate.IN)
circuit.addWire(in1, FixedLocation.IO, b, NotGate.IN)
circuit.addWire(in2, FixedLocation.IO, c, NotGate.IN)
circuit.addWire(a, NotGate.OUT, b, NotGate.IN)
circuit.addWire(a, NotGate.OUT, c, NotGate.IN)
circuit.addWire(b, NotGate.OUT, d, NotGate.IN)
circuit.addWire(c, NotGate.OUT, d, NotGate.IN)
circuit.addWire(d, NotGate.OUT, e, NotGate.IN)
circuit.addWire(e, NotGate.OUT, out, FixedLocation.IO)This describes an XOR gate with NOT gate as the only primitive. It
has eight components and 10 wires—decently complex. A
FixedLocation component takes up 1 block of space and a NOT
gate takes up 2 blocks, with the input interface in one block and the
output in another. NOT gates can only be placed horizontally (i.e. 4
possible directions.)
Time to solve it:
val solver = MIPLayoutSolver()
val result = solver.solve(circuit, Vec3.inBox(Vec3(3, 2, 10)))I gave the solver a lot of slack: the feasibility space is \(3\times 2 \times 10\), considerably larger than what’s actually needed. Anyway, the code ran very fast (thanks to Gurobi). To visualize the result I wrote some extra code to generate an HTML which internally calls THREE.js:
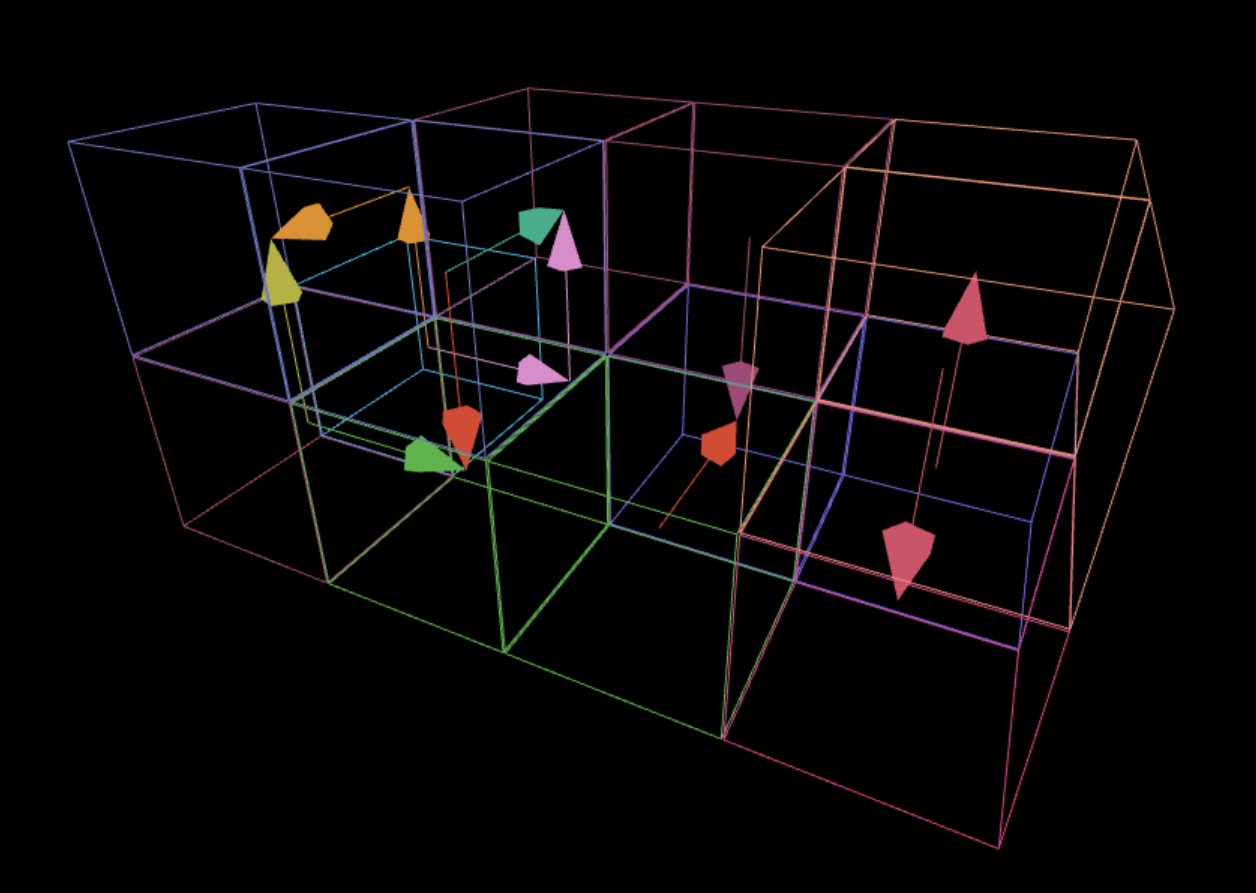
Complicated, isn’t it? The rightmost magenta block is the output
component out. The leftmost magenta block on the bottom
level is the input component in1. The cyan block next to
in1 is in2. And then blocks of the same color
represents a NOT gate, and arrows represent wires. The visualization is
a mess but I couldn’t do better without writing significantly more code.
If you try hard to follow the the arrows then you will find that this
routing is actually correct and does the exact thing the Kotlin
description above describes—and indeed, the circuit is amazingly
compact.
Yay!
(Note that here a component’s interface is connected to multiple wires. This might not be a good thing because by our constraints, if the fan in/out of any component is greater than 6, the constraint can not be satisfied. In an attempt to work around this I wrote a preprocessor that automatically introduces OR gates in circuit graphs when necessary. However, it turns out that with this modification things no longer work and the solver starts giving bogus results for some reason. I didn’t have time to investigate into this issue, but this could be an error in my ILP formulation somewhere!)
Afterwords—Two Years Later
Aha, I am finally here!
I did this project in 2020 but I somehow left this article unfinished for two years. What a shame! I spent an entire evening doing some archaeological work today and dug out my code and notes for this project (and confirmed they did work). The article is complete—finally—but please tolerate some inconsistencies in the writing. Everything after the AND gate example was written in 2022. Hopefully this article is helpful.
In retrospect, this small project is by no means complete. The test was too simple and I didn’t even make a Minecraft circuit out of the result! Probably too much handwaving. I could have of course went much much deeper if I hadn’t been busy with my college applications back then. I wrote the first part of this article on Nov. 25, 2020. A couple of days later I would have found myself rejected by Cornell. That was very frustrating then and I had to write more and more essays—I guess that was when this unfinished article got buried somewhere.
Anyway. it had been great fun doing this project and I learned a ton of interesting stuff despite the shallow progress on the surface. I still vividly recollect the moment I found in my inbox an email from the Gurobi China sales team because I was the first high school student in China to apply for an academic license and they really wanted to confirm I was not joking. I said that I was serious and several days later I got my license—that reply email literally made my day back then. Things have changed. When I re-install Gurobi to re-run my code last night, the Gurobi server recognized my MIT IP and gave me a license instantly. That was fast, but felt… different, certainly not as rewarding as before. I no longer play Minecraft as much as I did now, or do these fun projects as much as I had done. The decline in motivation on these things doesn’t seem to be a good sign to me. I can’t blame everything on the course load or UROP or anything else. It is a problem I am actively seeking a solution to.
