问题
自从 Office Lens,扫描全能王等 App 问世以来,人们越来越习惯使用手机代替扫描仪的功能来拍摄文档,而这些 App 对于一般的平面文档也确实起到了很好的效果。但是对于比较厚重的书本,由于页面向书籍弯折,拍摄到的页面往往是弯曲的,不仅影响美观也影响阅读体验。这些 App 也均没有针对这一情形进行特殊的优化。
例如:

如何在算法层面解决这个问题呢?
先前研究
这个问题的英文似乎是 Page Dewarping。以这个为关键词 Google 了一番,确实有一些相关的研究,但是几乎都是通过判断字的走向以及表格中直线的走向判断来判断纸的弯曲方向的。
除此以外,据我所知是有专门扫书的扫描仪的。原理是通过打一束激光,通过平直激光束在页面上的投影判断纸的弯曲方向。
但是我的手机没有激光发射器。我也不想识别文字方向,因为这大概率在实现上是一项艰苦的体力劳动。
能不能通过判断纸的边缘来计算纸的弯曲情况呢?
事情要一步一步来。
这一篇文章,我们就先探究如何从一副二维的图像重建纸面几个关键定点的三维坐标。
数学基础:透视投影
真的无论什么时候都是近大远小的吗?
众所周知,将三维空间当中的物体转变为二维空间中的像的过程被称作投影。
拍照显然就是一个投影的过程,因此在开始解决问题之前,我们先要确定投影的方式。
我们的眼睛,包括摄像头,获取到的画面之所以有着近大远小的特征,是因为无论是我们的眼睛,还是相机,采用的投影都是透视投影的缘故。透视投影的示意图如下:
如图所示,透视投影需要定义一个视点,即我们的眼睛或者相机感光元件所在的位置。然后所有远处物体反射到达视点的光线与一特定平面的交点,就是这一点所对应的投影点。
透视投影虽然是最符合直觉,也是最自然的投影方式,但是这并不意味着这就是唯一的投影方式。另一个较为常见的投影被称作正交投影。可以想象为透视投影中视点在无限远处的情形。(在正交投影当中,远近等大。也正是因为这个原因,正交投影广泛地被 CAD 软件所采用)因此,在对问题下手之前确定投影的类型是十分重要的。
OK,回到透视投影。之前的文字只给出了透视投影的定性叙述,这对于算法来说显然是不够的。透视投影可以在数学上可以如下定义:
假设投影平面是平面 \(z=0\),投影点是 \((0,0,-d)\)。
那么,对于三维空间中的点 \((x,y,z)\),透视投影将其唯一投影到二维平面中的 \((x^{\ast},y^{\ast})\)。其中
\[ \begin{aligned} x^{\ast}&=\frac{x}{1+z/d} \\ y^{\ast}&=\frac{y}{1+z/d} \end{aligned} \]
在现实当中,投影平面的大小是有限的,如果投影平面的大小是 \(w\times h\)(且以 \(z\) 轴为中心),那么 \(\theta_w=2\arctan\frac{w}{2d}\) 被称作水平方向上的视场(FoV),垂直方向上的视场定义类似。对于一个相同的摄像头,其视场一般可以看做一个常数(不同的焦距可能会导致些许变化)。以像素为单位,我的手机画幅是 \(3024\times 4032\),\(d\approx 3800\)。那么水平视场大概就在 \(45^{\circ}\) 左右。
在清楚透视投影的定义之后,这一篇文章的任务就变成了:
寻找满足一定约束条件的若干顶点的三维坐标,使其作为书页的边缘,其透视投影点恰对应图片上的点。
假设
为了适当简化问题,在此做出以下的假设:
纸页竖直的两边等长。
纸页竖直的两边平行。(注: 实际情况并不总是如此,但是让纸满足这个条件比把书压平总是容易得多了)
用户已经人工以某种形式标记出了图上一些关键点的坐标。即暂时不考虑自动检测书页(这也是一个大坑)。
明确问题
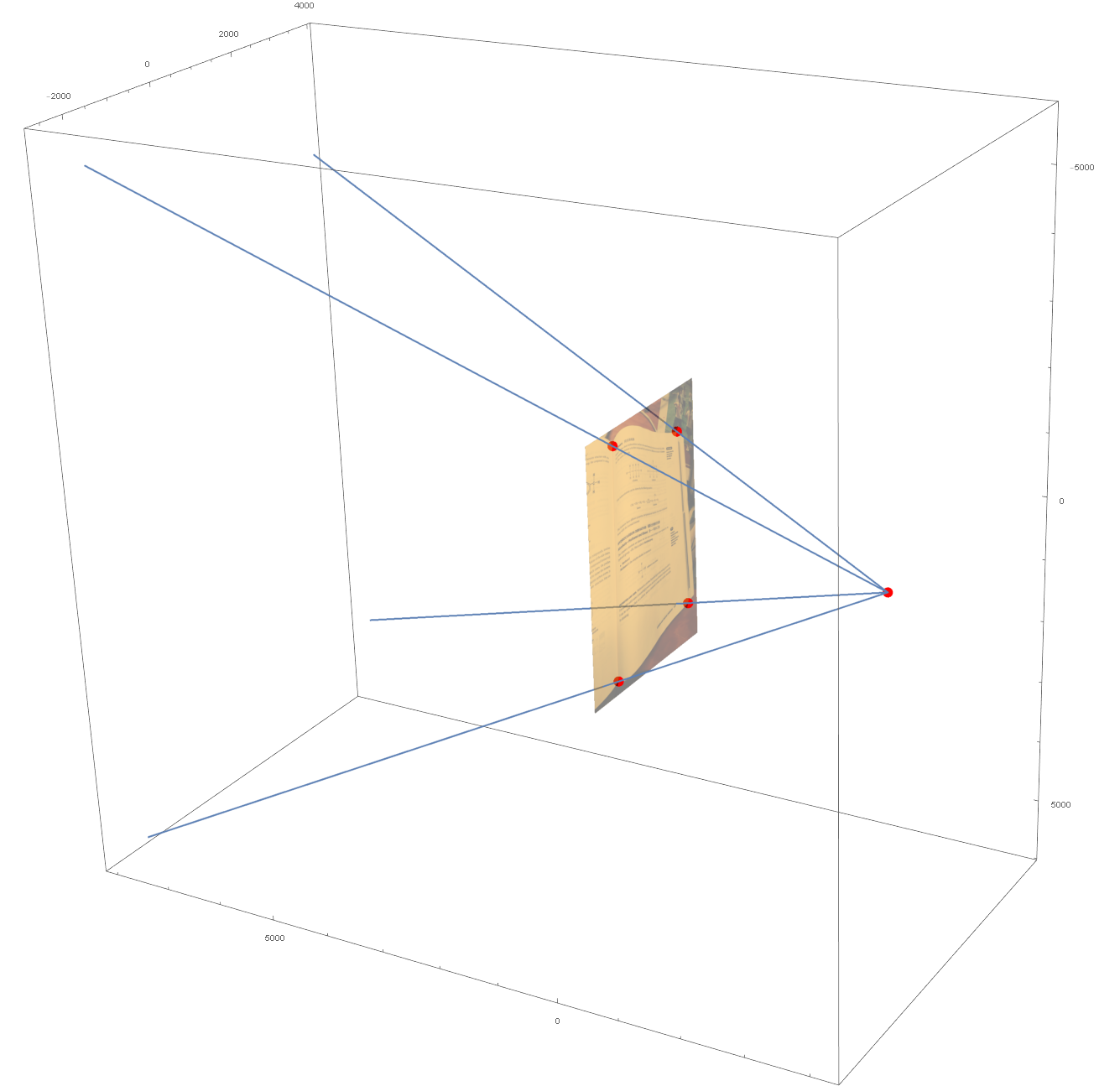
如下图所示:

我们已经手动标记出页面四角 \(A,B,C,D\) 的投影点 \(A^{\ast}(x_1,y_1),B^{\ast}(x_2,y_2),C^{\ast}(x_3,y_3),D^{\ast}(x_4,y_4)\)。在这篇文章当中我们的目标是反推出 \(A,B,C,D\) 以及平面。
假设 \(O\) 是坐标原点,以后会一直用 \(\vec{OP}\) 表示点 \(P\) 的坐标向量。
解决问题
算法直觉乱搞流
第一想法:啊?四个三维点?那就是 12 个参数咯?上启发式算法乱搞一波模拟退火遗传粒子群似乎就可以解决?当场否决
然后我们注意到投影点为定点的三维点的轨迹一定是一条过视点 \(P\) 的直线。 所以其实只有 4 个参数 —— 启发式算法成功可能性微存?
启发式优化算法毕竟不靠谱,我们还是一步一步来,比如说我们假设已经确定了 \(A\) 的 \(z\) 坐标 \(z_1\)(显然 \(A\) 的其他坐标也因此确定)。怎么确定我们暂且不管,反正最后大不了枚举。
然后呢?似乎还是没有头绪?
那我们继续假设已经确定了 \(B\) 的 \(z\) 坐标 \(z_2\)。怎么确定我们一样暂且不管。
现在我们已经可以算出 \(\vec{BA}\)。显然 \(\vec{CD}=\vec{BA}\),因此接下来只要我们知道 \(C\) 的坐标,\(D\) 的坐标随之确定。我们可以通过计算 \(D\) 投影点 \({D^{\ast}}'\) 和实际 \(D^{\ast}\) 的距离,得到我们解的误差 \(E\),即
\[ E={D^{\ast}}'D^{\ast} \]
那么怎么算出 \(C\) 的坐标呢?
这个时候直觉是一个好东西。我断定:误差 \(E\) 关于 \(C\) 的 \(z\) 坐标 \(z_3\) 单峰。
为什么?因为 \(C\) 的轨迹不是过 \(P\) 的直线吗,因此 \(D\) 经过 \(C\) 平移 \(\vec{CD}=\vec{AB}\) 的轨迹也是一条直线。直线的投影还是直线。 因此,当 \(z_3\) 增加,\(C\) 在直线上向后移动,\(D\) 也在直线上向后移动,其投影点 \({D^{\ast}}'\) 也在投影平面的直线上也一定沿某一特定方向移动。而二维平面内以个沿直线固定方向移动的点和直线外一定点 \(D^{\ast}\) 的距离显然是单峰的。证毕。
既然是单峰的,那么 \(C\) 的坐标就可以直接三分查找了呢,不用枚举 nice。
那么 \(B\) 的坐标呢?
直觉还是一个好东西。我再次断定:在 \(C\) 最优的情况下,误差 \(E\) 关于 \(B\) 的 \(z\) 坐标 \(z_2\) 单峰。
为什么?之前不是得到 \(D\) 的轨迹也是直线吗?当 \(B\) 前后移动时,\(\vec{BA}\) 也在变化。随着 \(\vec{BA}\) 的变化,经过 \(C\) 平移 \(\vec{BA}\) 得到的 \(D\) 的轨迹直线也在沿着某一方向平移(这个方向就是直线 \(BP\) 的方向)。那么 \({D^{\ast}}'\) 在投影平面上的轨迹直线也在沿着某一方向平移。而二维平面内沿着一个特定方向移动的直线到一定点的 \(D^{\ast}\) 的距离显然是单峰的。证毕。
哦豁,那么 \(B\) 的坐标也好三分了咯,又一次避免了枚举,nice。
为了三分的快一点,可以把三分的定比分点设成 \(\frac{3-\sqrt 5}{2}\),这样可以减少一半的计算次数(当然这就属于比较细节的优化了)。
接下来只剩下 \(A\) 了,\(A\) 需要枚举吗?
需要,也不需要。
直觉上来说 \(A,B,C,D\) 的坐标应当存在某种线性的关系,如下所示:
即无论 \(z_1\) 是多少,平面 \(ABCD\) 的总是不会发生变化的,因此我们只要随便选取一个 \(A\) 的坐标,通过二重三分把 \(B,C,D\) 算出来就行了。
看着不错,计算量也不高。但是…… 似乎依赖直觉的地方还是太多了。
之前论证单调性的过程的 insight 似乎暗示这问题的解析解应该不难?于是……
数学
设
\[ \vec{OA}=\begin{pmatrix} \lambda_1x_1\\ \lambda_1y_1\\ (\lambda_1-1)d \end{pmatrix}, \vec{OB}=\begin{pmatrix} \lambda_2x_2\\ \lambda_2y_2\\ (\lambda_2-1)d \end{pmatrix}, \vec{OC}=\begin{pmatrix} \lambda_3x_3\\ \lambda_3y_3\\ (\lambda_3-1)d \end{pmatrix} \]
则有:
\[ \vec{BA}=\begin{pmatrix} \lambda_1x_1-\lambda_2x_2\\ \lambda_1y_1-\lambda_2y_2\\ (\lambda_1-\lambda_2)d \end{pmatrix}\Rightarrow\vec{OD}=\vec{OC}+\vec{BA}=\begin{pmatrix} \lambda_3x_3-\lambda_2x_2+\lambda_1x_1\\ \lambda_3y_3-\lambda_2y_2+\lambda_1y_1\\ (\lambda_3-\lambda_2+\lambda_1-1)d \end{pmatrix} \]
那么其二维投影:
\[ \vec{OD^*}=\begin{pmatrix} \frac{\lambda_3x_3-\lambda_2x_2+\lambda_1x_1}{\lambda_3-\lambda_2+\lambda_1}\\ \frac{\lambda_3y_3-\lambda_2y_2+\lambda_1y_1}{\lambda_3-\lambda_2+\lambda_1} \end{pmatrix}=\begin{pmatrix} x_4\\ y_4 \end{pmatrix} \]
然后,就可以列方程:
\[ \begin{cases} \lambda_3x_3-\lambda_2x_2+\lambda_1x_1=(\lambda_3-\lambda_2+\lambda_1)x_4\\ \lambda_3y_3-\lambda_2y_2+\lambda_1y_1=(\lambda_3-\lambda_2+\lambda_1)y_4 \end{cases} \]
整理一下:
\[ \begin{cases} (x_2-x_4)\lambda_2-(x_3-x_4)\lambda_3=(x_1-x_4)\lambda_1\\ (y_2-y_4)\lambda_2-(y_3-y_4)\lambda_3=(y_1-y_4)\lambda_1 \end{cases} \]
也就是:
\[ \begin{pmatrix} \vec{OB}-\vec{OD} &\vec{OD}-\vec{OC} \end{pmatrix} \begin{pmatrix} \lambda_2\\ \lambda_3 \end{pmatrix}= (\vec{OA}-\vec{OD})\lambda_1 \]
最后只要解一下这个二元线性方程就可以了。
看来这个问题其实没有我想象的那样复杂啊。一开始直觉告诉我这东西解析解算起来很麻烦甚至不存在解析解,所以先从算法角度分析了一波。第二天开始想几个直觉结论的证明的时候才意识到似乎解析解不难算,后来发现正是如此。
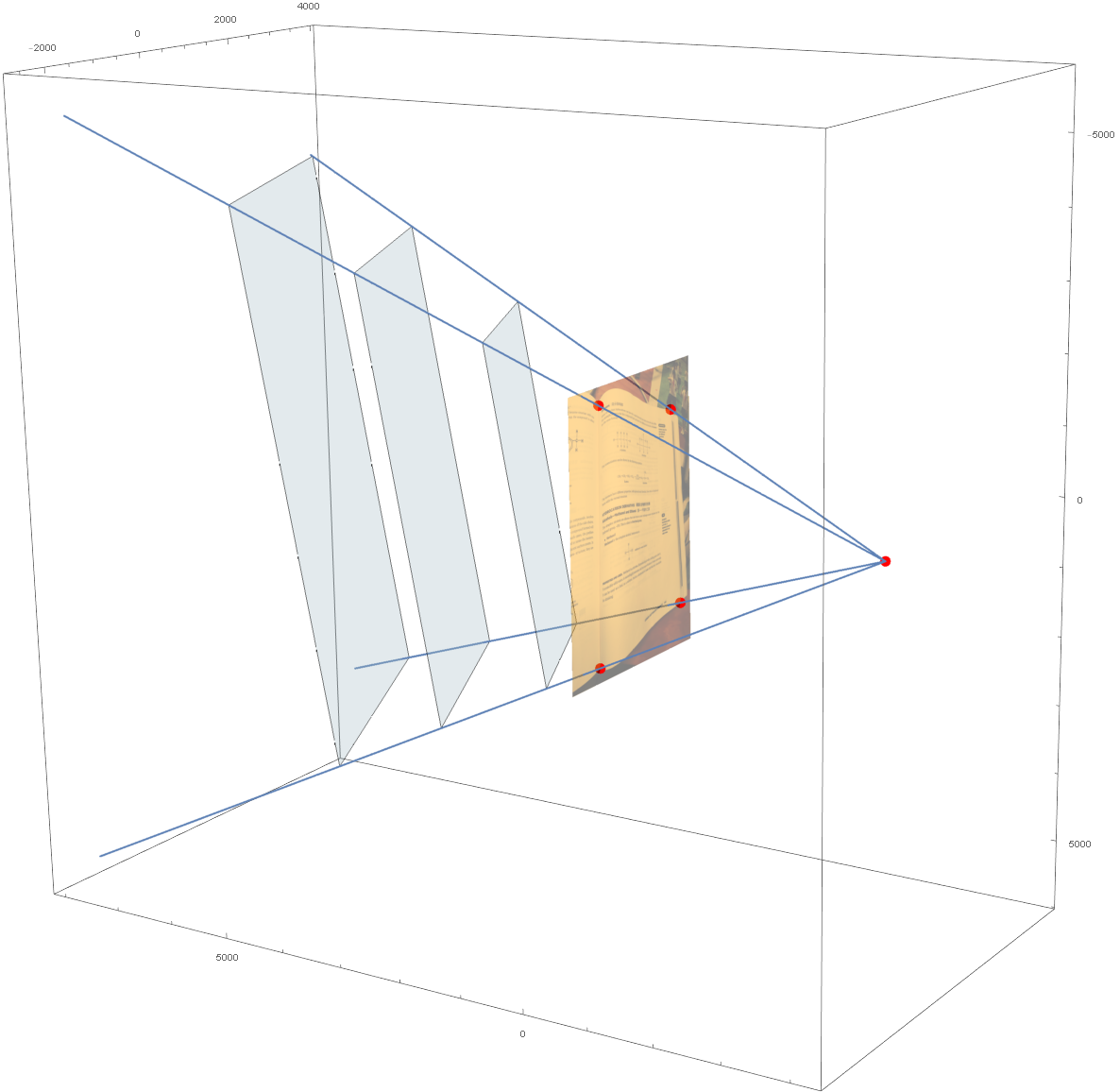
结果
最后的结果如下所示,加了法向量组成长方体证明确实这个建模没有问题。

下一篇文章大概会写如何基于这些信息计算纸面弯曲的参数方程吧……
但是手动标点这种东西四个点一个一个画图上查然后输入还可以忍受,标定横向边缘好几个点实在是懒啊…… 或许会先写一个标点的工具吧……