卷曲页面复原 2 ——曲线拟合

Posted on 2020-01-08 Views:

在前几天用扫描全能王的时候发现它似乎有自动拍书功能的（悲），似乎还可以自动识别，连标定都不要了。官方看到这个小博客的可能性微存？

但是那个是付费的会员功能！而且不管怎么样自己写一遍总归是有收获的。

进展！

过去的一周一直在和各种工程问题作斗争。目前的进展如下：

让这些探究只停留在Jupyter Notebook上我觉得太可惜了，加上我觉得自己经常会用，所以我准备撸一个App传到博客上去。

然后某人悲催地发现自己Web开发的技艺约等于0。

花了一个小时速成Vue和Vuetify，花了一个小时复习了一遍Node和JS，花了一个小时重装了Webstorm，Vue CLI开一个SPA直接开搞。

在Stack Overflow和Google和MDN里面转悠了五天之后自己终于写出了还算像样的雏形。现在标定功能已经写完了！

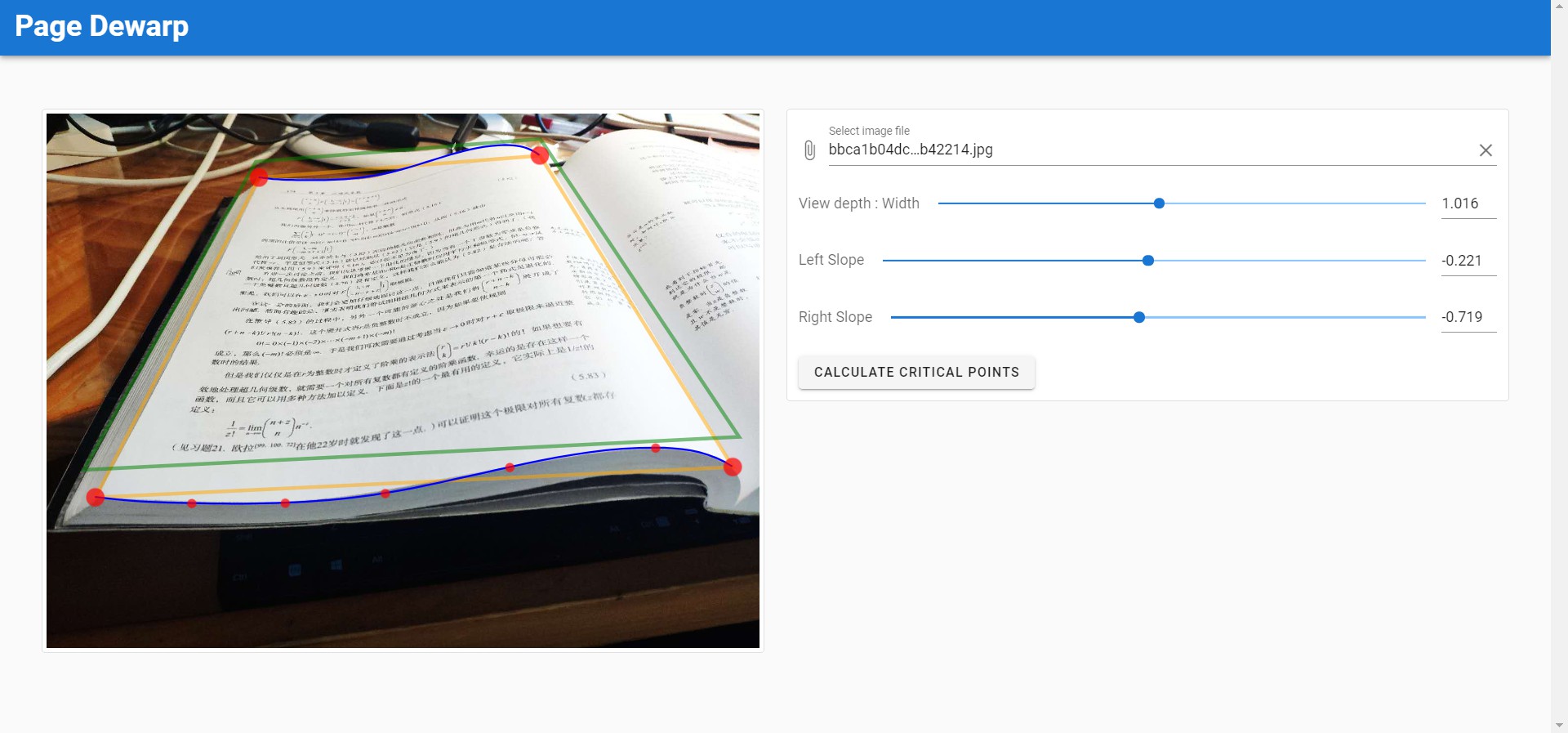
上图当中的黄框表示页面平面，绿框悬浮在黄框上面营造出一种透视立体的感觉（其实是调试完不想删掉了），上下两条蓝色的曲线表示书页的弯曲曲线。所有红色的点都是可以拖动的，拖动时还会在边角显示两倍放大后的特写便于精准定位，就像这样

功能上其实比上一篇文章没有多出多少（虽然在工程方面取得了巨大的突破）除了——曲线，这一条曲线其实没有那么简单。

反向投影

从上图可以看到，图中的曲线形状是由中间五个节点决定的，但是基于的是节点的三维坐标而不是所看到的二维坐标。这当中就牵涉到一个反向投影的问题——知道一个点在二维平面上投影点的坐标，如何在一定的约束条件下求取其三维坐标呢？

这个时候前一篇文章所做的页面平面重建的结果就变得重要了起来。这五个关键点都在书页的下边缘上，在数学上，五个小红点都在平面底边所在的，且垂直于平面的平面上。首先我们要确定这个平面，不妨称之为平面。

平面的方程式 Ax+By+Cz=D ， (A,B,C) 就是这个平面的法向量，我们已经知道了两个上的点（点和点），如果我们知道了平面的法向量，那么把点代入，方程当中的就出来了，平面就确定了。

在理想情况下，法向量就是 $\vec{AB}$ ，因为理想情况下 $\vec{AD}\perp\vec{AB}$ 。

但是现实比较残酷，由于计算的一点点小误差，算出来的 $\vec{AD}$ 并不总是垂直于 $\vec{AD}$ ，比如说夹角是 $89.94^{\circ}$ 。这个 $\vec{AB}$ 就不是法向量了，这是很坑的。我一开始偷懒把 $\vec{AB}$ 当法向量写到程序里面去，结果调试的时候一直有小误差，心态都快崩了。

然后我才意识到果然不能偷懒，正确的法向量就是 $\vec{AD}\times(\vec{AD}\times\vec{AB})$ 。

然后对于在平面上的任意一个点 Q(x, y,z) ，已知其投影是 $Q^{\ast}(x^{\ast},y^{\ast})$ 。根据方程

$\begin{cases} Ax+By+Cz=D\\ x=x^{\ast}(1+z/d)\\ y=y^{\ast}(1+z/d) \end{cases}$

就能把这个点的坐标算出来了。

之后还需要再做一步，把 $\vec{AQ}$ 分解：

$\vec{AQ}=a\vec{AD}+b\frac{\vec{AD}\times\vec{AB}}{\left|\vec{AD}\times\vec{AB}\right|}\quad a\in[0,1]$

之后得到的 (a,b) 才是一个相对归一化了的坐标。使用这个坐标进行插值的话， A,B,C,D 四个点小范围内的运动都不会改变曲线的形状，这相当于增加了我们算法的鲁棒性。

插值

使用什么曲线插值比较好呢？

如果在计算机的背景下最先想到的肯定是贝塞尔曲线，但是贝塞尔曲线不经过它控制点，这似乎在界面上就不是那么直观。

如果采用高阶多项式的插值呢？那么Runge现象又会非常严重，可以预见效果会很差。

于是乎我采用的是三次样条插值。对于三次样条插值：

假设有个节点，那么就有个区间，对应条曲线，个参数。
对于一条三次曲线，其两个端点的值是确定的，那么就有个约束条件。
中间的个节点上相邻的三次曲线必须一阶导连续且二阶导连续，那么就是个约束条件。
为了能够在大多数情况下求出所有参数的准确值，还需要个约束条件。

似乎最常见的边界条件被称为自然边界条件。也就是样条曲线两端的二阶导为。Wiki上介绍的算法也是针对这种边界条件设计的，但是在我们这个情境下自然边界似乎不适用，因为书页的一侧总是向下凹向书脊，书脊起了固定作用。我一开始照抄Wiki上的算法结果曲线对不上翻车了。

这个情景应该用的似乎是夹持边界条件。也就是人为地给出曲线两端的一阶导。也就是我的界面右侧出现"Left Slope"和"Right Slope"两个slider的原因。这个边界条件试下来似乎和实际吻合得还是相当不错的。问题主要出现在算法这里，我虽然从矩阵的形式推断一定存在像Wiki上处理自然边界条件一样显式线性的算法，但是自己还是懒得去推了直接用mathjs的lusolve函数（Well 我相信mathjs这种大库的消元一定有优化……），速度还是非常令人满意的，但是代码可读性就是一个比较大的问题了：

let n = nodes.length - 1; // nodes.length knots, so nodes.length - 1 ranges and piecewise curves

let A = zeros(4 * n, 4 * n); // 4 parameters for each curve
let b = zeros(4 * n);
for (let i = 0; i < n; i++) {
    // Equation 4i and 4i + 1 ensures continuity of the spline
    b.set([4 * i], nodes[i][1]);
    for (let j = 0; j < 4; j++)
        A.set([4 * i, 4 * i + j], pow(nodes[i][0], j));
    b.set([4 * i + 1], nodes[i + 1][1]);
    for (let j = 0; j < 4; j++)
        A.set([4 * i + 1, 4 * i + j], pow(nodes[i + 1][0], j));
    if (i < n - 1) {
        // Equation 4i + 2 and 4i + 3 ensures continuity of both the 1st and 2nd derivative
        A.set([4 * i + 2, 4 * i + 1], 1);
        A.set([4 * i + 2, 4 * i + 2], 2 * nodes[i + 1][0]);
        A.set([4 * i + 2, 4 * i + 3], 3 * pow(nodes[i + 1][0], 2));
        A.set([4 * i + 2, 4 * i + 5], -1);
        A.set([4 * i + 2, 4 * i + 6], -2 * nodes[i + 1][0]);
        A.set([4 * i + 2, 4 * i + 7], -3 * pow(nodes[i + 1][0], 2));
        A.set([4 * i + 3, 4 * i + 2], 2);
        A.set([4 * i + 3, 4 * i + 3], 6 * nodes[i + 1][0]);
        A.set([4 * i + 3, 4 * i + 6], -2);
        A.set([4 * i + 3, 4 * i + 7], -6 * nodes[i + 1][0]);
    }
}
// Equation 4n - 2 and 4n - 1 set constraint on slope on both ends
A.set([4 * n - 2, 1], 1);
A.set([4 * n - 2, 2], 2 * nodes[0][0]);
A.set([4 * n - 2, 3], 3 * pow(nodes[0][0], 2));
b.set([4 * n - 2], this.leftSlope);
A.set([4 * n - 1, 4 * n - 3], 1);
A.set([4 * n - 1, 4 * n - 2], 2 * nodes[n][0]);
A.set([4 * n - 1, 4 * n - 1], 3 * pow(nodes[n][0], 2));
b.set([4 * n - 1], this.rightSlope);
let sln = lusolve(A, b);

虽然加了注释但是代码只能用悲剧来形容了（悲）。

全怪mathjs的API，我个人认为如果用Julia来写的的话一定没有那么多事情（确信）。

最后的效果倒确实是极好的。