这篇笔记写于 2019/2/15,原供稿班级公众号,在某人决定博客重更之后重新整理发上来~2019/12/8 上传
[TOC]
为什么会有这篇文章?
最近网上也都在吹爆《流浪地球》这部科幻片啊……
然后我自己前几天也慕名去电影院看了一下,感觉特效之类的着实过瘾。但是作为一部定位为硬科幻的科幻片,除去画面以外,科学的严谨性还是很重要的。但是这部片子里面的一些科学设定在一个 KSP 玩家看来似乎……

还是有些槽点呢…… 当然瑕不掩瑜。这篇文章就稍微指出一点我发现的《流浪地球》当中的一些 Bug,这些 Bug 主要是轨道力学上的,也就当给同学们做一个科普吧。
自己也是半瓶水,所以,欢迎指正。
定性吐槽
电影里面的运动学乍一看是非常符合直觉的。比如说:
- 地球的发动机一关,整个地球马上就往木星上靠过去了,轨道一下子拐了一个弯
- 空间站发动机一开,整个空间站马上就直线飞离地球了,轨道上看得一清二楚
- 要引爆空间站,就直接对准目标直线冲刺过去了
似乎没啥问题咯?
Uhmmmmmm……
这么说的话以下二位的棺材板就要压不住了:

(牛顿)

(开普勒)
为啥嘞?
开普勒第一定律
回忆一下我们第一学期学的牛顿第一定律:
牛顿第一定律:假若某物体所受合外力为零,则该物体的运动速度不变,即保持静止或做匀速直线运动。
如果所受合力不是零,而是一直受到一个定质点的引力作用,物体的运动状态又会是怎样呢?
开普勒结合牛顿的万有引力定律对牛顿第一定律进行了拓展,得出了开普勒第一定律:
开普勒第一定律:每一个行星都沿各自的椭圆轨道环绕太阳,而太阳则处在椭圆的一个焦点中。
开普勒定律刻画的行星在只受太阳引力作用下的稳定运动轨道,但是真的只有椭圆这一种吗?
其实定律实际推导出的轨道是圆锥曲线,即圆,椭圆,抛物线或双曲线中的任意一种,只是对于普通行星来说,后面两种轨道意味着飞掠而不是围绕,不符合实际,因此开普勒在定律表述里面便只说 “椭圆”。
那知道这个定律有啥用呢?
发动机不需要一直点火!
首先,如果地球的行星发动机的推力够足,理论上是用不着像电影里面一直点火的,我们只需要在地球轨道附近把地球加速到足够高速然后熄火,那么根据开普勒定律,地球自己会沿一条圆锥曲线被甩离太阳,并在木星附近被木星捕获,沿以木星为焦点的抛物线或双曲线掠过木星进行引力弹弓加速,然后离开木星被甩出太阳系!这段过程中理想情况下地球只受星体引力影响,不需要发动机一直点火,除了进行一定的轨道修正!‘
这个操作有没有实例呢?
且看旅行者二号:

它在被火箭加速到足够高的速度之后就放飞自我了,之后走的轨道是什么样的呢?
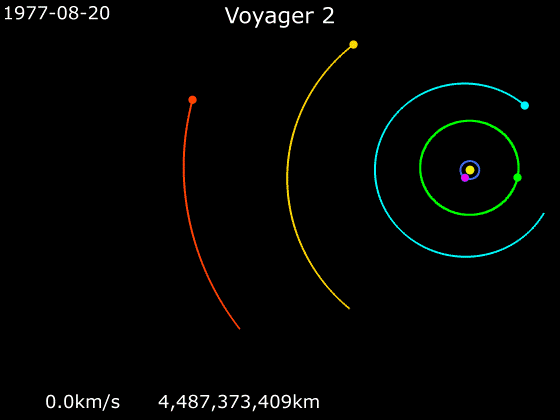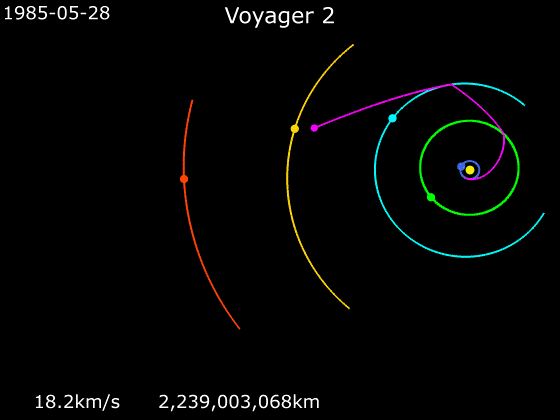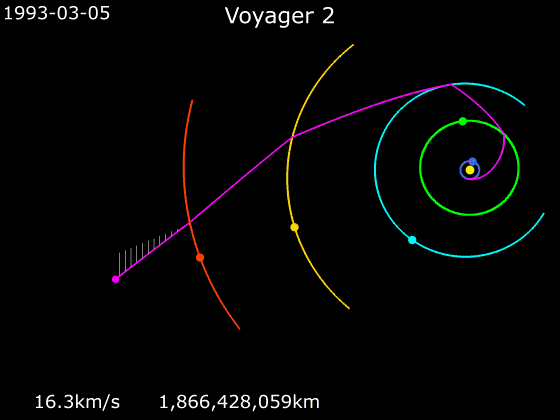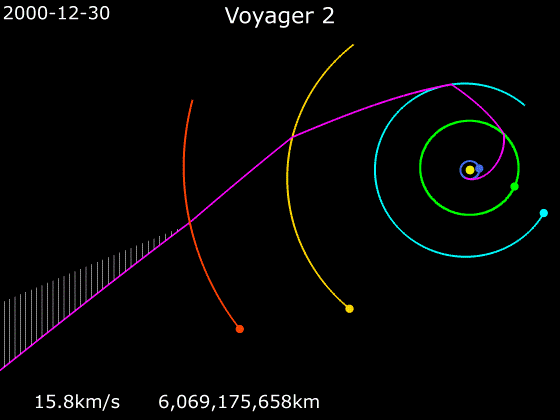
(绿色为木星轨道)
在离开地球的十多年里,旅行者 2 号几乎没有启用过自己的轨道发动机,包括在飞掠火星木星等星体进行引力加速的时候也是如此。如果它是靠电影中的一直加速才飞到那么远的话,试问这么小的机体燃料放哪里呢?
所以看到地球上的行星发动机一直燃烧了十七年,Emmm… 编剧开心就好。(当然不排除是加速度过低导致需要持续加速的情况,这种情况下轨道确实比较难算,出偏差也是正常的,因此这其实不算一个特别大的 Bug)
熄火 / 点火之后的轨道不科学!
看过电影的同学应该记得,在行星发动机一半熄火的时候,地球马上就拐了一个弯,从飞掠木星变成栽进木星了,就好像有什么东西让它大幅度减速了一样。编剧在这里似乎混淆了速度和加速度的概念,就算地球发动机全部停机,地球几乎只受木星引力作用,地球也会沿着熄火前最后一刻所处的抛物线轨道继续运行:

(图找的不是熄火的那个场景,只做演示用)
也就是说,地球会继续按照 “原轨道” 的红线运行,而不是像影片中的那样当场轨道一拐拐到蓝色轨道上去了。
也就是说,其实发生影片中所谓 “危机” 的概率会小非常多。
什么?你说抛物线和双曲线本来就有一个拐点?那和影片当中的形状和位置都对不上好吗?
同样的,空间站准备开溜时候的轨道也注定不是一条直线,它同时受着地球和木星的引力影响,做的是三体运动,轨迹怎么会那么漂亮呢?
因为这样,空间站要开到地木之间引爆,也绝非一个 “前进三!” 的直线冲刺能够与解决的,复杂着呢!
定量吐槽
小马在看完电影的当晚估算了一下:
然后第二天就有同学告诉我我仿佛漏算了什么…… 确实是这样的,那这个定量的估算到底是怎么来的呢?
Tsiolkovsky 公式
在 1903 年,俄罗斯科学家齐奥尔科夫斯基推导出了著名的火箭公式: \[ \Delta v = v_e \ln \left(\frac{m_0}{m_1}\right) \] (详细推导见这里)
其中 \(v_e\) 表示火箭工质的喷出速度,\(m_0\) 表示火箭的初始质量,\(m_1\) 表示火箭的燃烧后的末质量,\(\Delta v\) 表示火箭在发动机加速过程当中所获得的速度增量。
什么叫工质喷出速度呢?“工质” 就是火箭发动机喷嘴喷出的物质的代称,也是火箭发动机推力的来源:发动机给工质一个力将工质高速推离火箭,反作用力同时给火箭一个巨大的动力。
如果假设地球的质量是 \(m_e\),石头的质量是 \(m_f\),那么在我们的情况下,公式可以写作: \[ \Delta v = v_e \ln \left(\frac{m_e}{m_e-m_f}\right) \] 我们可以非常简单地估算出(或者借助网络查阅到)\(m_e\) 的值,因此只要我们知道了 \(v_e\) 和 \(\Delta v\),我们就可以由上式反解 \(\frac{m_f}{m_e}\)。从而算出作为燃料的石头的重量!
计算 \(\Delta v\)
直接逃逸
我们首先计算如果不借助木星的引力弹弓效应需要的最小 \(\Delta v\) 大概是多少:
首先我们计算在地球轨道上相对太阳的逃逸速度,取太阳的标准重力参数 \(\mu = GM = 1.327124 \times 10^{20} \mathrm{m^3/s^2}\),取地日平均距离 \(r_e = 1\mathrm{au} = 1.496 \times 10^{11} \mathrm{m}\),若假设轨道偏心率极小可以忽略不计,则根据机械能守恒逃逸速度可以计算如下: \[ \begin{aligned} v_{es} &= \sqrt{\frac{2\mu}{r_e}} \\ &= \sqrt{\frac{2\times 1.327124 \times 10^{20} \mathrm{m^3/s^2}}{1.496 \times 10^{11} \mathrm{m}}} \\ &\approx 42.126\mathrm{km/s} \end{aligned} \] 我们当然不用取 \(\Delta v = 42.126\mathrm{km/s}\),因为地球绕太阳公转本来就有一定的线速度,地球的轨道速度如下: \[ v_o = \sqrt{\frac{\mu}{r_e}} = \frac{v_{es}}{\sqrt 2} \approx 29.784\mathrm{km/s} \] 如果行星发动机顺着地球的公转方向加速,则 \(\Delta v = v_{es} - v_o = 12337.1 \mathrm{m/s}\) 就够了。
借助木星
我们接下来估算一下如果借助木星的引力弹弓效应加速大约需要多少 \(\Delta v\)。
因为没有给定地木之间的位置关系,直接算引力弹弓难度极大不会,但是我们可以估算一下 \(\Delta
v\) 的下界:我们假设地球只需要在地球轨道和木星轨道之间执行一次霍曼转移来进行交会。即让地球的椭圆轨道与木星轨道内切。基于 Vis-viva 公式,取木星轨道半径为近日点的 \(r_j = 7.405 \times
10^{11}\mathrm{m}\),则在地球轨道上加速所需要的 \(\Delta v\) 为: \[
\begin{aligned}
\Delta v &= \sqrt{\frac{2\mu r_j}{r_e(r_e + r_j)}} - v_o \\
&= \sqrt{\frac{2\times 1.327 \times 10^{20} \mathrm{m^3/s^2} \times
7.405 \times 10^{11}\mathrm{m}}{1.496 \times 10^{11} \mathrm{m}\times
(1.496 \times 10^{11} \mathrm{m} + 7.405 \times 10^{11}\mathrm{m})}} -
29.784\mathrm{km/s} \\
&\approx 8634.71 \mathrm{m/s}
\end{aligned}
\] (假设地木轨道共面,不然还要修正轨道倾角)
也就是说,就算地球不是想借助木星加速,只是想碰到木星的轨道,都需要这么多的 \(\Delta v\),要借助木星加速一般轨道会更大一点,因此我们估算出来的是 \(\Delta v\) 的下界。
发动机种类
我们已经算出了 \(\Delta v\) 的大小,接下来让我们估一下 \(v_e\) 的大小,我们同时会计算出来所需要燃料的质量。
在下文中,取地球质量为 \(m_e = 5.97\times10^{24}\mathrm{kg}\),岩石密度为 \(\rho = 3000\mathrm{kg/m^3}\)。
目前科技
目前人类能够造出的 \(v_e\) 最高(比冲最高)的化学燃料发动机大概是液氢液氧发动机,\(v_e \approx 4400\mathrm{m/s}\)。(根据资料比冲最高的发动机其实是欧空局的 DS4G(电推),\(v_e \approx 210000\mathrm{m/s}\),可惜推力只有 \(2.5\mathrm{N}\),还贼费电。)
因此,在直接逃逸的情况下我们有: \[ \begin{aligned} &\quad \Delta v = v_e \ln \left(\frac{m_e}{m_e-m_f}\right) \\ &\Rightarrow \ln \left(\frac{m_e}{m_e-m_f}\right) = \frac{\Delta v}{v_e} \\ &\Rightarrow \frac{m_e-m_f}{m_e} = e^{-\frac{\Delta v}{v_e}} \\ &\Rightarrow m_f = \left(1 - e^{-\frac{\Delta v}{v_e}}\right)m_e \end{aligned} \] 取相关数据带入,得 \(m_f = 5.608 \times 10^{24}\mathrm{kg} \approx 94\%m_e\)……
Ummm…… 不用算了,要把地球挖空的。
在借助木星引力加速的情况下其实也好不到哪里去,计算可以得到 \(m_f = 5.131 \times 10^{24}\mathrm{kg} \approx 86\%m_e\)。
这个好一点,思考一下人类靠 \(14\%\) 的地球可以干嘛吧,这还没算上后续的加速和减速,估计流浪到最后变成小行星了。细思极恐
以上计算其实反映出一点:因为逆用公式算出的只是燃油质量和火箭质量的比值,这个比值无论大到地球小到火箭都适用,也就是说大家看到巨大的火箭一般都有 \(95\%\) 以上的质量是燃料,而剩下的质量包括了外壳,发动机,管线,最后才是载荷。
外星科技
既然影片当中的发动机叫 “重聚变发动机”(先不纠结为啥重元素可以不吸能聚变),那推进方式肯定不是垃圾的氢氧机可以比拟的。这样吧,假设工质可以加速到光速(顺便压住了爱因斯坦的棺材板),取 \(v_e = c = 299792458\mathrm{m/s}\)。会怎么样呢?(关于相对论效应:齐奥尔科夫斯基公式只有在被推进物接近光速(Relativistic Rocket)的时候才需要修正,对于工质速度接近光速的情况则不用。)
在直接加速的情况下,我们有 \(m_f = 2.45673 \times 10^{20}\mathrm{kg} \approx 4.1\times 10^{-5}m_e\)。似乎还可以接受哦?
体积是多少呢? \[ V_f = \frac{m_f}{\rho} = 8.19\times10^{16}\mathrm{m^3}\approx (434.256\mathrm{km})^3 \] 也就是说所需要的燃料可以装满一个边长 \(434\mathrm{km}\) 的立方体!作为参考,国际空间站轨道高度为 \(400\mathrm{km}\) 左右。
如果嫌这个不够直接,取陆地地壳平均厚度 \(33\mathrm{km}\),则需要挖掉整个面积为 \(2.5 \times 10^{12}\mathrm{m^2}\) 大小的土地,而全球陆地面积才只有 \(1.49\times 10^{14}\mathrm{m^2}\)!这意味着:
- 大概要把全球陆地都下挖 \(550\mathrm{m}\) 左右,比环球金融中心高一点。
- 把边长为 \(1575\mathrm{km}\) 的一块正方形地壳挖光,作为参考,这约占我国国土的四分之一。
利用木星加速需要多少燃料呢?带入可得 \(m_f = 1.71947 \times 10^{20}\mathrm{kg}\),可以装满边长为 \(385\mathrm{km}\) 的立方体。需要把全球陆地都下挖 \(400\mathrm{m}\) 左右,如果打算把地壳挖光,则需要挖去的地壳面积为我国国土的五分之一左右。
Emm……Emm……
质能转化角度
换种思想,假设人类已经解锁了一个无敌恐怖的科技点,即把燃料的所有静能量转化为地球的机械能,那会怎么样呢?
根据著名的质能方程式 \(E=mc^2\),我们可以列式: \[ m_fc^2 = \frac{1}{2}m_e(v_o + \Delta v)^2 - \frac{1}{2}m_ev_o^2 \] 如果直接逃逸,解得燃料质量为 \(m_f = 2.94629 \times 10^{16} \mathrm{kg}\)。获取这么多燃料需要把整个上海市区的地壳挖空。
如果借助木星。解得燃料质量为 \(m_f = 1.95593 \times 10^{16} \mathrm{kg}\)。获取这么多燃料也需要把整个上海中心城区的地壳挖空。
这样开起来稍微可行一点了吧…… 似乎开掘一万座地下城挖剩的石料就够用了?
但是这个视角的问题在于我们的假设,如果静能量全部转化成机械能,则:
- 燃料必须在相互反应当中全部湮灭,作为对比,核聚变和核裂变当中湮灭的仅仅是反应物和产物之间的微小质量差(可能是每个原子一两个中子 / 质子),目前能够达到全部湮灭的方法只有把当中一半的燃料转化为反物质。
- 湮灭产生的巨大能量必须全部收集,不能产生耗散。
- 收集的能量必须全部转化成地球的机械能,这意味着不能有喷出的工质,因为这相当于有能量转化成工质机械能,同时整个体系必须不能发热,也发动机必须全部常温,不然会有热量作为热能耗散。
这当中做到任何一点都是科技的极大进步,而但凡物质不能全部湮灭(而是采取核聚变),能量难以完全收集与转化,则能量的利用率只会千万倍地往下降,消耗的燃料也必将回归上一小节当中的恐怖水平。
结语
经过上文的分析,我们发现其实流浪地球的世界观本身还是有一点不科学的,尤其是地球发动机,简直是 Bug 一般的存在。但是这并不是说流浪地球就不是一部好片子,因为几乎每一部科幻片都有能让人杠一杠的地方。因此写这篇文章只是为了分享一下自己想法,也帮助科普一下一些轨道力学的知识。当然在推式子的过程中也和同学们复习了一下指对数函数的知识,真是极好的。
安利
什么?你问我自己怎么会想到这些?
因为本人是 Kerbal Space Program 玩家啊 #(滑稽)

在这里给大家安利一下这款 “游戏”,游戏本身非常硬核,需要玩家自己设计并且发射航天器进入轨道,自己规划轨道计算燃料,自己操控交会对接,模拟了近乎真实的物理系统,内有一个类似太阳系的星系。上述 \(\Delta
v\) 的计算,霍曼转移,燃料量的计算都是游戏当中的必修课是的现在玩游戏都要用计算器。个人认为比一些纯粹娱乐向的手游之类的更能从中学到知识,但同时因为这款游戏玩起来消耗大量脑细胞与时间,一般每周末玩两个小时就够了。
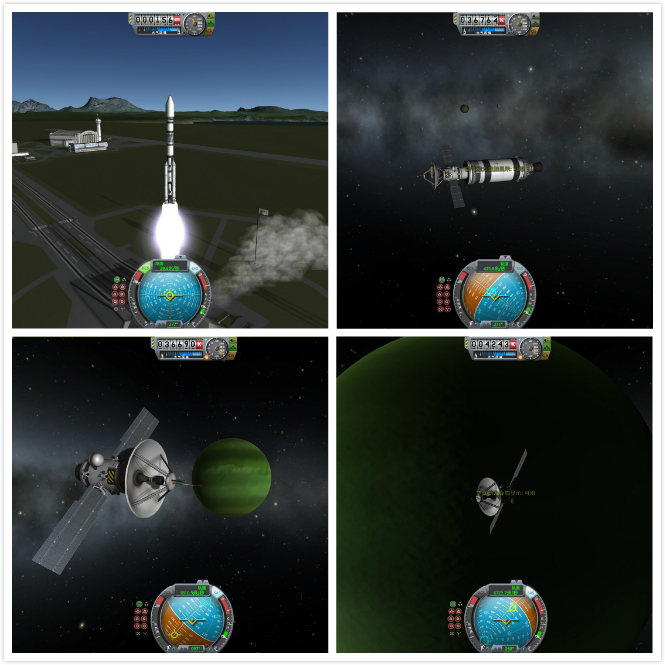
(我自己搭的 Jool 飞掠器的截图,Jool 对应太阳系的木星)
从动手设计到发射成功现实当中花了一个半小时,游戏当中是两年半,失败五次。本质新手劝退向游戏
当然,虽然这款游戏 Steam 上要七十多块,但是破解版烂大街。欢迎有兴趣的同学来玩。
数据来源
大部分公式,数据均来源于英文维基百科,少部分来自 NASA 官网。
公式全部基于万有引力定律与能量守恒定律,绝大部分的公式可以在高中知识下进行推导。