线性代数四大空间笔记

Posted on 2021-04-29 Views:

以下是读Gilbert Strang的Introduction to Linear Algebra的后回忆整理的笔记。内容大概包括第三节和第四节开头的一部分。

四大空间

对于矩阵 $A\in \mathbb{R}^{m\times n}$ ，定义

的列空间为其所有列向量的张成空间，的列向量的线性组合记作 $A\boldsymbol{x}=\boldsymbol b$ ——因此所有这个形式的 $\boldsymbol b$ 都属于的列空间。记作。 $C(A)\subset\mathbb{R}^m$ 。
的零空间为令其列向量线性组合为零的组合构成的空间，即所有满足 $A\boldsymbol{x}=\boldsymbol 0$ 的向量 $\boldsymbol x$ 。记作。 $N(A)\subset \mathbb{R}^n$ 。
的行空间为其所有行向量的张成空间。因为的行向量都是 $A^{\mathrm{T}}$ 的列空间，所以行空间可以记作 $C\left(A^{\mathrm T}\right)$ 。 $C\left(A^{\mathrm T}\right) \subset \mathbb{R}^{n}$ 。
的左零空间为令其行向量线性组合为零的组合构成的空间，即所有满足 $\boldsymbol{x}^{\mathrm T}A = \boldsymbol 0^{\mathrm T}$ 的向量 $\boldsymbol{x}$ ，现在 $\boldsymbol x$ 在左边，所以和零空间相比就叫左零空间了。左零空间自然可以记作 $C\left(A^{\mathrm T}\right)$ 。 $C\left(A^{\mathrm T}\right) \subset \mathbb{R}^{m}$ 。

以上就是线性代数当中比较重要的四个空间。虽然有四个，但本质只有“列空间”和“零空间”两种。基于矩阵的定义是颇有些枯燥的。矩阵只是线性变换比较常用且典型的形式，列空间和零空间的定义并不局限于此。归根结底，列空间是线性变换的“值域”，零空间是线性变换的“零点”。

_{注：列空间在一些地方也叫做像空间（image），零空间在一些地方也叫做核（kernel）。个人认为，对于一般的线性变换，像空间的称谓比列空间更为恰当，但kernel这个词就有些莫名奇妙——我没有了解过相关的背景，但我觉得零空间的叫法更为直观。}

向量空间的维度

向量空间的维度定义为这个空间任何一组基包含的向量个数。这个定义蕴含的一个事实是：对于同一个向量空间，无论其基如何选取，其大小都是相同的。这里摘录一个书上的证明：

证明： 假设向量空间 $\mathbf V$ 的两组基为 $\boldsymbol{v_1},\boldsymbol{v_2},\cdots,\boldsymbol{v_n}$ 和 $\boldsymbol{w_1}, \boldsymbol{w_2}, \cdots ,\boldsymbol{w_m}$ 。运用反证法，不失一般性，设 n < m 。因为 $\boldsymbol{v_1},\boldsymbol{v_2},\cdots,\boldsymbol{v_n}$ 是基，所以任意 $\boldsymbol{w_k}$ 都可以用他们的线性组合表示。即

$\boldsymbol{w_k} = \begin{bmatrix} \boldsymbol{v_1} &\boldsymbol{v_2} &\cdots &\boldsymbol{v_n} \end{bmatrix}\cdot \boldsymbol{a}$

（回忆一下，矩阵左乘向量等于按照向量的系数对矩阵的列向量进行线性组合）

进一步地，

$\begin{bmatrix} \boldsymbol{w_1} &\boldsymbol{w_2} &\cdots &\boldsymbol{w_m} \end{bmatrix}= \begin{bmatrix} \boldsymbol{v_1} &\boldsymbol{v_2} &\cdots &\boldsymbol{v_n} \end{bmatrix}\cdot A$

不难发现，

是

行

列的矩阵，而

，所以

是扁的。在代数上，齐次线性方程组的变量多于方程数，也就是说 $A\boldsymbol{x} = \boldsymbol{0}$ 有非平凡解。

$\begin{aligned} A\boldsymbol{x} &= \boldsymbol{0} \\ \Rightarrow \begin{bmatrix} \boldsymbol{v_1} &\boldsymbol{v_2} &\cdots &\boldsymbol{v_n} \end{bmatrix} A\boldsymbol{x} &= \boldsymbol{0} \\ \Rightarrow \begin{bmatrix} \boldsymbol{w_1} &\boldsymbol{w_2} &\cdots &\boldsymbol{w_m} \end{bmatrix} \boldsymbol{x} &= \boldsymbol{0} \end{aligned}$

也就是说， $\boldsymbol{w_1}, \boldsymbol{w_2}, \cdots ,\boldsymbol{w_m}$ 线性相关，推出矛盾，证毕。

四大空间的维度

一个矩阵四大空间的维度可以通过将其化简为行简化阶梯型（reduced row echelon form）来计算。行简化阶梯型的定义

阶梯型/上三角型矩阵
主元位置都是
主元正上方都是

例如

$\operatorname{rref}\left( \begin{bmatrix} 1 &1 &2 &4\\ 1 &2 &2 &5\\ 1 &3 &2 &6 \end{bmatrix} \right) = \begin{bmatrix} 1 &0 &2 &3\\ 0 &1 &0 &1\\ 0 &0 &0 &0 \end{bmatrix}$

行简化阶梯型矩阵可以通过原矩阵的初等行变换得到（高斯消元）。

行简化阶梯型矩阵当中主元的个数称为矩阵的秩（rank）。我们首先注意到，对于一个行简化阶梯型矩阵，

它列空间的维度是它的秩：主元列显然是线性无关的，而非主元列显然可以用主元列的线性组合表示（系数就写在列里面呢，比如说在上面的例子中，第四列是第一列的倍和第二列的倍之和）。
它行空间的维度也是它的秩：行简化阶梯型的形态让我们不难发现每一个非零行都是线性无关的。原因在于每个非零行都包含一个主元，而只有那一行在主元的那一列是。
它零空间的维度是列数与秩之差，即非主元列的个数：从方程 $A\boldsymbol x = \boldsymbol 0$ 的角度看，非主元列代表自由变量。通过令一个自由变量为，令其余自由变量为，并依此计算主元，我们可以得到和自由变量同样数目的若干“解向量”。这些解向量线性无关，都处在零空间中，且张成整个零空间，因此是零空间的一个基。
它左零空间的维度是行数与秩之差，即零行的个数：非零行线性无关，因此要使行的线性组合为零所有非零行的系数必须为零，零行的系数任意，因此左零空间的维度就是零行的个数。

接下来，我们观察到从一般矩阵化简为行简化阶梯型的过程不会改变矩阵的四个空间的维度：

初等行变换不会改变列向量之间的线性关系——对于所有列来说，行变换是“一荣俱荣，一损俱损”的。如果原来矩阵的第三列是第一列的两倍，那么行变换之后第三列还是第一列的两倍。如果原来矩阵的第二列是第一列和第三列的和，那么行变换之后这个和的关系不变。
因为列向量之间的线性关系没有变，所以零空间不会变，列空间的维数也不会变（但列空间本身会变）。
行变换是对行的线性组合，所以行简化阶梯型的行空间是原矩阵行空间的子集；而高斯消元的行变换是可逆的，所以原矩阵的行空间也是行简化阶梯型行空间的子集。因此，化简到行简化阶梯型的过程当中，行空间不变。
行简化阶梯型只是揭示而并非改变行向量之间的线性相关关系（行简化阶梯型中的零行表示原来的行向量和上面几行的行向量线性相关）。原来线性无关的行不会因为行变换就线性相关，反之亦然。因此左零空间的维数是不会变的。

所以，一般矩阵的秩也就可以定义为其对应行简化阶梯形矩阵的秩，一般矩阵的四大空间的维度也可以用其秩计算了。

四大空间维度的奇妙关联

简要地总结一下，对于一个行列秩的矩阵，有

$\dim\left(C(A)\right) = r$
$\dim\left(N(A)\right) = n - r$
$\dim\left(C\left(A^{\mathrm T}\right)\right) = r$
$\dim\left(N\left(A^{\mathrm T}\right)\right) = m - r$

然后我们整理一下就发现

$\begin{aligned} \dim\left(C(A)\right) + \dim\left(N(A)\right) &= n = \dim\left(\mathbb{R}^n\right) \\ \dim\left(C\left(A^{\mathrm T}\right)\right) + \dim\left(N\left(A^{\mathrm T}\right)\right) &= m = \dim\left(\mathbb{R}^m\right) \end{aligned}$

有什么意义？注意到

可以看作一个线性变换，其定义域所在的空间是 $\mathbb{R}^n$ 。 $A^{\mathrm T}$ 也是如此。结合零空间和列空间的意义，我们发现了这样一个关系：

线性变换定义域（输入）的维度，等于零空间与值域（输出）维度之和。

好理解不？一个输入的部分维度在线性变换中“卷入零空间”消失了，只有剩下的维度反映在输出中。

高屋建瓴，妙不可言。这个关系具有震撼人心的力量。自己前几天在学校阅览室读到这一行，差点拍案叫绝。

线性代数是简洁的。

线性代数是优美的。

莫不如是。

这有啥用处？

书后有一个习题

定义两个子向量空间 $\mathbf{V}$ 和 $\mathbf W$ 的和 $\mathbf{V} + \mathbf{W}$ 为二者中任意向量组合形成的空间（即二者基的并的张成空间）。

求证：
$\dim(\mathbf V) + \dim(\mathbf W) = \dim(\mathbf V + \mathbf W) + \dim(\mathbf V \cap \mathbf W)$

朴素的做法设出两向量空间交的基，然后在此基础上分别拓展形成 $\mathbf V$ ， $\mathbf W$ ，然后再证明这些分别拓展的基和两空间交的基一起是线性无关的。步骤倒也不是特别复杂。

但是格局低了。

Mike Artin提出的证明是这样的：考虑二元运算把二元组 $(\boldsymbol v\in \mathbf V, \boldsymbol w\in \mathbf W)$ 变换到 $\boldsymbol v + \boldsymbol w$ 。易证这个变换是线性的。其输入维度是 $\dim(\mathbf V) + \dim(\mathbf W)$ 。其值域的维度是 $\dim(\mathbf V + \mathbf W)$ 。其零空间是 $(\boldsymbol v, \boldsymbol -v)$ 其中 $v\in \mathbf V \cap \mathbf W$ ，维度自然是 $\dim(\mathbf V \cap \mathbf W)$ 。因为线性变换输入的维度等于输出的维度与零空间维度之和，得证。

太高了，我恐高症都犯了。

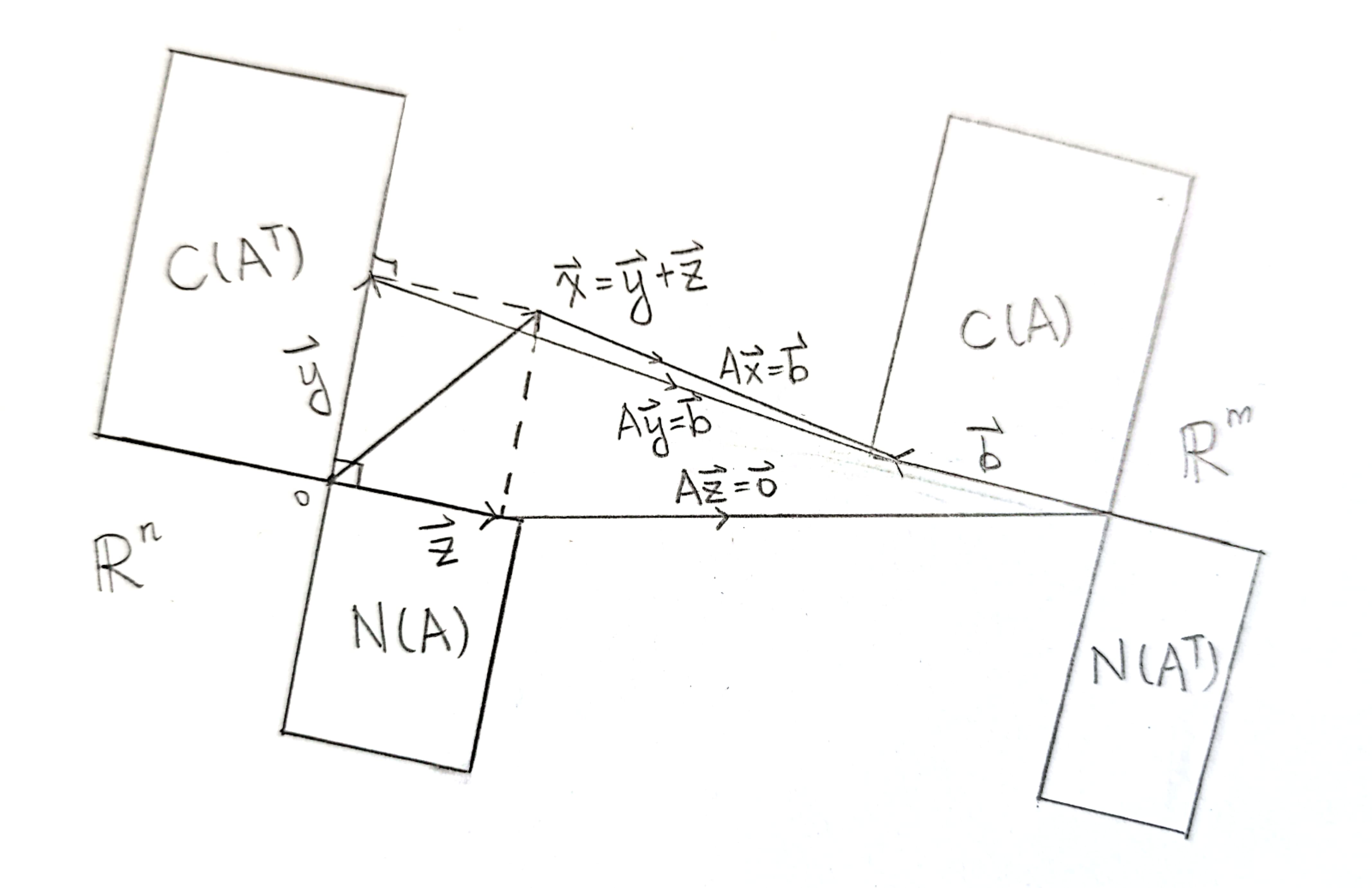
四大空间的正交性

还有一点很妙的是：四大空间是两两正交的！

什么是正交？两个子向量空间正交当且仅当两个空间中的任意两个向量都互相垂直。（说“子向量空间”是因为两个向量谈论垂直不垂直的前提条件自然是两个向量维数一样，即同属于一个更大的向量空间）

在 $\mathbb R^n$ 内，零空间和行空间 $C\left(A^{\mathrm T}\right)$ 互相正交
$\forall A^{\mathrm T}\boldsymbol x \in C\left(A^{\mathrm T}\right),\boldsymbol y \in N(A),\quad \left(A^{\mathrm T}\boldsymbol x\right)^{\mathrm T}\boldsymbol y = \boldsymbol{x}^{\mathrm T}A\boldsymbol y = \boldsymbol{x}^{\mathrm T}\cdot \boldsymbol 0 = 0$
又因为二者维度之和为，所以二者互补，即 $N(A) + C\left(A^{\mathrm T}\right) = \mathbb{R}^n$ 。
在 $\mathbb R^m$ 内，列空间和左零空间 $N\left(A^{\mathrm T}\right)$ 互相正交
$\forall A\boldsymbol x \in C(A),\boldsymbol y \in N\left(A^{\mathrm T}\right),\quad \left(A\boldsymbol x\right)^{\mathrm T}\boldsymbol y = \boldsymbol{x}^{\mathrm T}A^{\mathrm T}\boldsymbol y = \boldsymbol{x}^{\mathrm T}\cdot \boldsymbol 0 = 0$
又因为二者维度之和为，所以二者互补，即 $C(A)+ N\left(A^{\mathrm T}\right) = \mathbb{R}^m$ 。

于是就可以祭出Introduction to Linear Algebra 封面上的神图~~手绘重制以表敬意~~